Optimization 101优化入门
一个简单的问题
一个非常简单的问题,如何用最少的材料做一个容积为1m³的圆柱形容器?在把圆柱形容器简化为等厚的金属板并忽略接头的成本和材料耗损可以把问题描述为:一个圆柱体容器,在容积为1m³的条件下,表面积最小,应该如何选择尺寸?
1app = BucketOptApp;
2exportgraphics(app.ContainerAxes, "bucket.png")
这个问题的对象(系统)非常简单,是一个静态对象,可以用两个参数来描述,分别是底面半径和高度,这都是很自然的几何参数。
$$ S_p = \{r, h\} $$我们要问的问题或者说要求解的问题是一个最小化的问题,当然难点在于还有一个约束。
$$ \begin{split} \arg\min_{S_p} \quad & A \\ \text{s.t.} \quad & V = 1 \end{split} $$通过简单的几何知识,有如下数学模型:
$$\left\{ \begin{split} &V = \pi r^2 h \\ &A = 2\pi r h + 2 \pi r^2 \end{split} \right. $$符号求解
简单问题简单解
这个题目相当简单,在约束关系$V=1$中可以求解得到$h=\frac{1}{\pi r^2}$,代入$A$的表达式中,可以得到:
$$ A = 2\pi r \frac{1}{\pi r^2} + 2 \pi r^2= \frac{2}{r} + 2 \pi r^2 $$这是一个二次函数,类似于一个碗,最小值点很容易通过求解方程$\frac{dA}{dr}=0$得到。
$$ r_\text{min} = \sqrt[3]{\frac{1}{2\pi}} \approx 0.5419 $$对应的$h_\text{min}$自然可以得到。
$$ h_\text{min} = 2 \sqrt[3]{\frac{1}{2\pi}} = 2 r \approx 1.0839 $$自行上难度用Matlab
那我们非要用Matlab做怎么整呢?符号运算工具箱还是很好用的(现在)。
1%% define symbols
2syms r h V(r,h) A(r, h)
3V(r, h) = pi * r * r * h;
4A(r, h) = 2 * pi * r * h + 2 * pi * r * r;
5
6% 这两个很节省计算,也算是灵巧的小手,一定要学会约束条件提前给进去
7assume(r > 0);
8assume(h > 0);
9
10constraint = V == 1;
11
12%% solve h and subs to A
13hr = solve(constraint, h);
14Ar = subs(A, h, hr);
15
16r_min = solve(diff(Ar, r) == 0);
17
18assert(subs(diff(Ar, r, r), r, r_min) > 0);
19
20%% report result
21h_min = subs(hr, r_min);
22
23pretty(simplify(h_min))
24pretty(simplify(r_min))
首先,我们在第2行到第4行把问题输进去;第7~8行我们做了一个约束,两个几何量都大于零,这是为了去掉那些复数的解。下面这个例子,可以看到约束函数assume的作用。
1 >> syms x; solve(x^3 == 1)
2 ans =
3 1
4 - (3^(1/2)*1i)/2 - 1/2
5 (3^(1/2)*1i)/2 - 1/2
6 >> syms r; assume(r>0); solve(r^3 == 1)
7 ans =
8 1
第10行中,我们定义了一个约束。符号工具箱中,用==来表示方程中的等于。这在下面描述要求解的方程中也能用得到。
首先我们符号求解$h$(第12-13行)。
1 >> hr
2 hr =
3 1/(r^2*pi)
然后第14行,把求解得到的$h(r)$代入面积公式,求解极值点(第16行),最后还要验算是否是最小值点(第18行)。
最后,我们把$h_\text{min}$也求出来,并打印在终端。
Lagrange multiplier a.k.a. 拉格朗日乘子法
当然,对于约束优化问题,还有一个常用的方式就是拉格朗日乘子法。
$$ \begin{split} \arg\min_{x} \quad & f(x) \\ \text{s.t.} \quad & g(x) = 0 \end{split} $$我们利用拉格朗日乘子$\lambda$把问题写为无约束优化:
$$ \arg\min_{x} \quad f(x) + \lambda g(x) $$1%% solve with constraints
2syms lambda
3L(r, h, lambda) = A + lambda * (V - 1);
4
5result = solve(diff(L, r)==0, diff(L, h)==0, diff(L, lambda)==0)
我们非常暴力地把约束条件和优化目标写在一起构成一个新的函数:
$$ L(r, h, \lambda) = A(r, h) + \lambda \left[V(r, h) - 1\right] $$然后求解方程组:
$$ \begin{cases} \frac{dL}{dr} = 0 \\ \frac{dL}{dh} = 0 \\ \frac{dL}{d\lambda} = 0 \end{cases} $$最后得到结果:
1 >> result
2 result =
3 struct with fields:
4
5 h: 2*(1/(2*pi))^(1/3)
6 lambda: -4*pi*(1/(2*pi))^(2/3)
7 r: (1/(2*pi))^(1/3)
实际上,我甚至能够无聊到编一个界面来演示这个桶的优化的过程。
演示App
界面
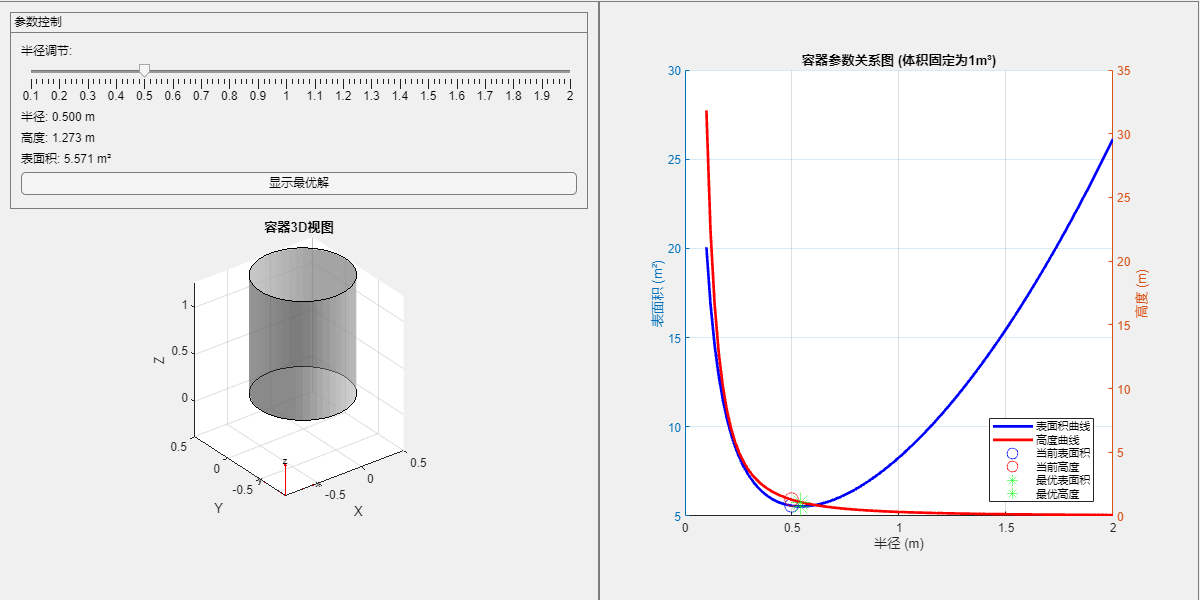
在这个界面里,我们可以用滑块来调节容器的底面半径,界面上同步显示容器的形状,和高度、表面积的值。UI右边是一个坐标系,分别绘制高度和面积曲线,调节过程中,红色与蓝色的圈圈表示当前半径对应的值。
1exportgraphics(app.PlotAxes, "curve.png")
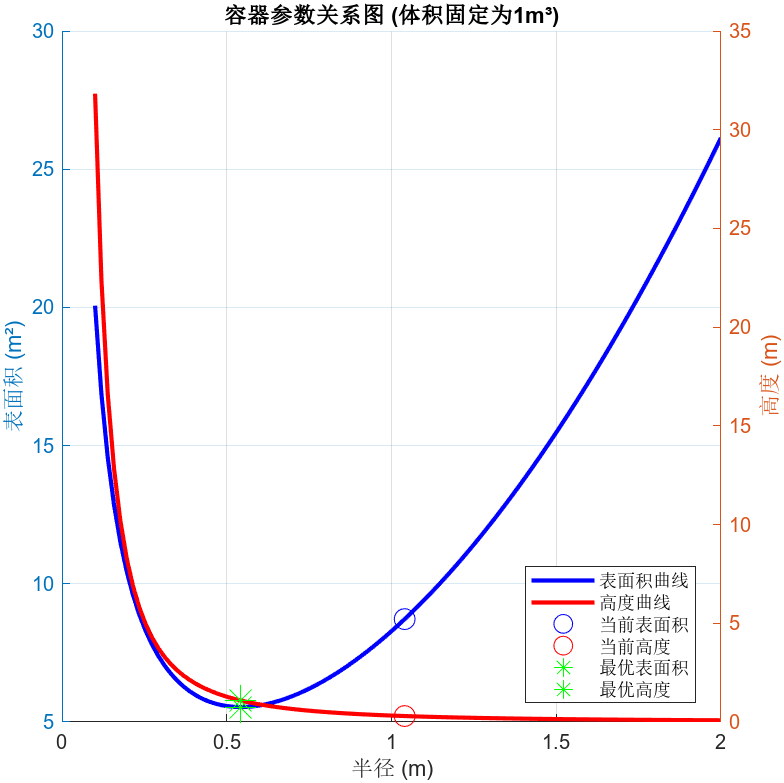
当然,我们还提供了一个设置显示最优解的按钮。只能说,无聊的人类会干出无聊的事情。
拖动半径滑块,看看当半径变得非常大后,容器的高度会变得非常小,而表面积会变得非常大。
1exportapp(app.UIFigure, "flat.png")
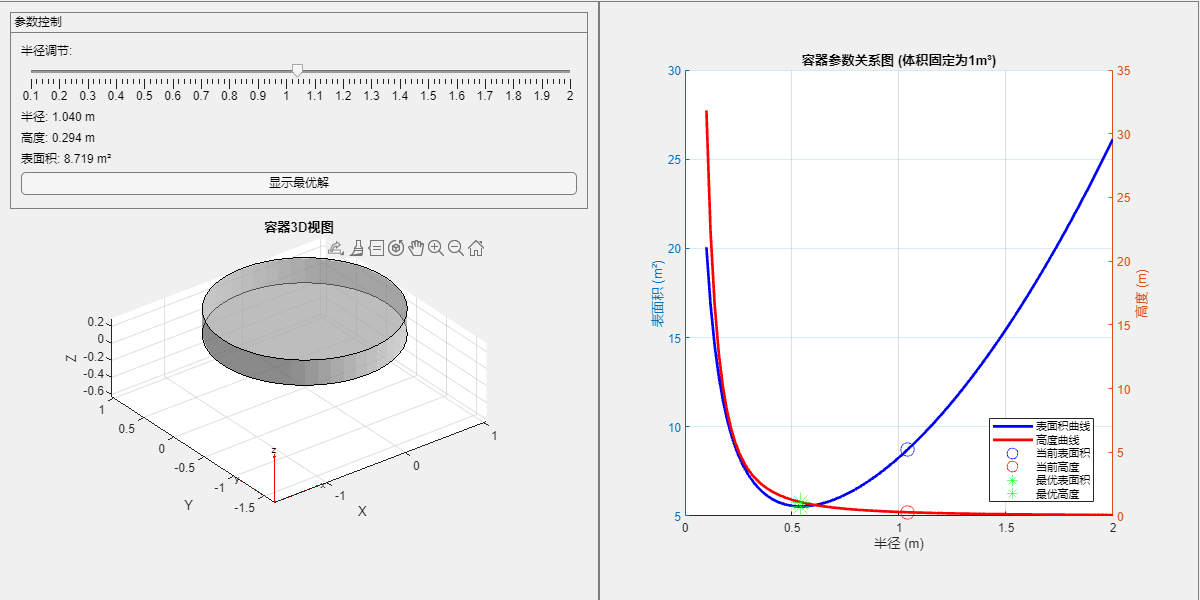
源代码
1classdef BucketOptApp < matlab.apps.AppBase
2 % 一个显示简单容器优化的App
3 % 整个界面分为两栏
4 % 界面左边是圆柱形容器的两个参数的滑动调节和容器3D显示
5 % 界面右边是设计数值图形,是一个两个y坐标的图
6 % 横坐标为地面半径
7 % 左边的纵坐标是圆柱体的表面积的大小
8 % 右边的纵坐标是高度
9 % 约束条件:圆柱体体积为1
10
11 % Properties that correspond to app components
12 properties (Access = public)
13 UIFigure matlab.ui.Figure
14 LeftPanel matlab.ui.container.Panel
15 RightPanel matlab.ui.container.Panel
16 LeftGrid matlab.ui.container.GridLayout
17 ContainerAxes matlab.ui.control.UIAxes
18 ControlPanel matlab.ui.container.Panel
19 RadiusSlider matlab.ui.control.Slider
20 RadiusLabel matlab.ui.control.Label
21 RadiusValue matlab.ui.control.Label
22 HeightValue matlab.ui.control.Label
23 SurfaceAreaValue matlab.ui.control.Label
24 OptimalButton matlab.ui.control.Button
25 PlotAxes matlab.ui.control.UIAxes
26 end
27
28 properties (Access = private)
29 % 默认参数
30 DefaultRadius = 0.5 % 默认半径
31 MaxRadius = 2.0 % 最大半径
32 MinRadius = 0.1 % 最小半径
33 Volume = 1.0 % 固定体积为1
34 HasPDEToolbox % 是否安装了PDE工具箱
35 OptimalRadius % 最优半径
36 end
37
38 methods (Access = private)
39 % 根据半径计算高度(保持体积为1)
40 function h = calculateHeight(app, r)
41 h = app.Volume / (pi * r^2);
42 end
43
44 % 计算表面积
45 function A = calculateSurfaceArea(app, r, h)
46 A = 2 * pi * r * h + 2 * pi * r^2;
47 end
48
49 % 更新3D容器显示
50 function updateContainer(app)
51 r = app.RadiusSlider.Value;
52 h = calculateHeight(app, r);
53 A = calculateSurfaceArea(app, r, h);
54
55 % 清除当前axes
56 cla(app.ContainerAxes)
57
58 if app.HasPDEToolbox
59 % 创建圆柱体几何体
60 gm = multicylinder(r, h);
61 % 绘制几何体
62 pdegplot(gm, 'Parent', app.ContainerAxes, 'FaceAlpha', 0.5)
63 else
64 % 使用基本绘图函数绘制圆柱体
65 % 创建圆柱体侧面
66 [X,Y,Z] = cylinder(r, 50);
67 Z = Z * h;
68
69 % 绘制侧面
70 surf(app.ContainerAxes, X, Y, Z, 'FaceAlpha', 0.5)
71 hold(app.ContainerAxes, 'on')
72
73 % 绘制底面
74 theta = linspace(0, 2*pi, 50);
75 [X,Y] = pol2cart(theta, r);
76 Z = zeros(size(X));
77 fill3(app.ContainerAxes, X, Y, Z, 'b', 'FaceAlpha', 0.5)
78
79 % 绘制顶面
80 Z = ones(size(X)) * h;
81 fill3(app.ContainerAxes, X, Y, Z, 'b', 'FaceAlpha', 0.5)
82 hold(app.ContainerAxes, 'off')
83 end
84
85 % 设置视角和标题
86 view(app.ContainerAxes, 3)
87 title(app.ContainerAxes, '容器3D视图')
88 xlabel(app.ContainerAxes, 'X')
89 ylabel(app.ContainerAxes, 'Y')
90 zlabel(app.ContainerAxes, 'Z')
91 axis(app.ContainerAxes, 'equal')
92 grid(app.ContainerAxes, 'on')
93
94 % 更新显示值
95 app.RadiusValue.Text = sprintf('半径: %.3f m', r);
96 app.HeightValue.Text = sprintf('高度: %.3f m', h);
97 app.SurfaceAreaValue.Text = sprintf('表面积: %.3f m²', A);
98 end
99
100 % 更新数值图表
101 function updatePlot(app)
102 r = app.RadiusSlider.Value;
103 h = calculateHeight(app, r);
104
105 % 清除当前axes
106 cla(app.PlotAxes)
107
108 % 创建半径数组
109 r_array = linspace(app.MinRadius, app.MaxRadius, 100);
110
111 % 计算对应的表面积和高度
112 h_array = app.Volume ./ (pi * r_array.^2); % 根据体积约束计算高度
113 A_array = 2 * pi * r_array .* h_array + 2 * pi * r_array.^2; % 表面积 = 2πrh + 2πr²
114
115 % 创建双y轴图
116 yyaxis(app.PlotAxes, 'left')
117 p1 = plot(app.PlotAxes, r_array, A_array, 'b-', 'LineWidth', 2);
118 ylabel(app.PlotAxes, '表面积 (m²)')
119
120 yyaxis(app.PlotAxes, 'right')
121 p2 = plot(app.PlotAxes, r_array, h_array, 'r-', 'LineWidth', 2);
122 ylabel(app.PlotAxes, '高度 (m)')
123
124 xlabel(app.PlotAxes, '半径 (m)')
125 title(app.PlotAxes, '容器参数关系图 (体积固定为1m³)')
126 grid(app.PlotAxes, 'on')
127
128 % 标记当前点
129 hold(app.PlotAxes, 'on')
130 yyaxis(app.PlotAxes, 'left')
131 p3 = plot(app.PlotAxes, r, 2 * pi * r * h + 2 * pi * r^2, 'bo', 'MarkerSize', 10);
132 yyaxis(app.PlotAxes, 'right')
133 p4 = plot(app.PlotAxes, r, h, 'ro', 'MarkerSize', 10);
134
135 % 标记最优点
136 r_opt = app.OptimalRadius;
137 h_opt = calculateHeight(app, r_opt);
138 A_opt = calculateSurfaceArea(app, r_opt, h_opt);
139 yyaxis(app.PlotAxes, 'left')
140 p5 = plot(app.PlotAxes, r_opt, A_opt, 'g*', 'MarkerSize', 15);
141 yyaxis(app.PlotAxes, 'right')
142 p6 = plot(app.PlotAxes, r_opt, h_opt, 'g*', 'MarkerSize', 15);
143 hold(app.PlotAxes, 'off')
144
145 % 添加图例
146 legend(app.PlotAxes, [p1, p2, p3, p4, p5, p6], ...
147 '表面积曲线', '高度曲线', '当前表面积', '当前高度', '最优表面积', '最优高度', ...
148 'Location', 'best')
149 end
150 end
151
152 % Callbacks that handle component events
153 methods (Access = private)
154 % 半径滑块值改变回调
155 function RadiusSliderValueChanged(app, ~)
156 updateContainer(app)
157 updatePlot(app)
158 end
159
160 % 最优解按钮回调
161 function OptimalButtonPushed(app, ~)
162 app.RadiusSlider.Value = app.OptimalRadius;
163 updateContainer(app)
164 updatePlot(app)
165 end
166 end
167
168 % Component initialization
169 methods (Access = private)
170 % 创建UI组件
171 function createComponents(app)
172 % 检查是否安装了PDE工具箱
173 app.HasPDEToolbox = license('test', 'PDE_Toolbox');
174
175 % 计算最优半径
176 app.OptimalRadius = (1/(2*pi))^(1/3);
177
178 % 创建UIFigure
179 app.UIFigure = uifigure('Visible', 'off');
180 app.UIFigure.Position = [100 100 1200 600];
181 app.UIFigure.Name = '容器优化App (体积固定为1m³)';
182
183 % 创建左右面板
184 app.LeftPanel = uipanel(app.UIFigure);
185 app.LeftPanel.Position = [0 0 600 600];
186
187 app.RightPanel = uipanel(app.UIFigure);
188 app.RightPanel.Position = [600 0 600 600];
189
190 % 创建左侧网格布局
191 app.LeftGrid = uigridlayout(app.LeftPanel, [2 1]);
192 app.LeftGrid.RowHeight = {'fit', 'fit'};
193 app.LeftGrid.Padding = [10 10 10 10];
194 app.LeftGrid.RowSpacing = 10;
195
196 % 创建3D显示区域
197 app.ContainerAxes = uiaxes(app.LeftGrid);
198 app.ContainerAxes.Layout.Row = 2;
199 app.ContainerAxes.Layout.Column = 1;
200
201 % 创建控制面板
202 app.ControlPanel = uipanel(app.LeftGrid);
203 app.ControlPanel.Layout.Row = 1;
204 app.ControlPanel.Layout.Column = 1;
205 app.ControlPanel.Title = '参数控制';
206
207 % 创建控制面板网格布局
208 controlGrid = uigridlayout(app.ControlPanel, [6 1]);
209 controlGrid.RowHeight = {'1x', 'fit', '1x', '1x', '1x', 'fit'};
210 controlGrid.Padding = [10 10 10 10];
211 controlGrid.RowSpacing = 5;
212
213 % 创建参数显示区域
214 app.RadiusLabel = uilabel(controlGrid);
215 app.RadiusLabel.Layout.Row = 1;
216 app.RadiusLabel.Layout.Column = 1;
217 app.RadiusLabel.Text = '半径调节:';
218
219 app.RadiusSlider = uislider(controlGrid);
220 app.RadiusSlider.Layout.Row = 2;
221 app.RadiusSlider.Layout.Column = 1;
222 app.RadiusSlider.Limits = [app.MinRadius app.MaxRadius];
223 app.RadiusSlider.Value = app.DefaultRadius;
224 app.RadiusSlider.ValueChangedFcn = @(s,e) RadiusSliderValueChanged(app, e);
225
226 % 创建参数值显示标签
227 app.RadiusValue = uilabel(controlGrid);
228 app.RadiusValue.Layout.Row = 3;
229 app.RadiusValue.Layout.Column = 1;
230 app.RadiusValue.Text = sprintf('半径: %.3f m', app.DefaultRadius);
231
232 app.HeightValue = uilabel(controlGrid);
233 app.HeightValue.Layout.Row = 4;
234 app.HeightValue.Layout.Column = 1;
235 app.HeightValue.Text = sprintf('高度: %.3f m', calculateHeight(app, app.DefaultRadius));
236
237 app.SurfaceAreaValue = uilabel(controlGrid);
238 app.SurfaceAreaValue.Layout.Row = 5;
239 app.SurfaceAreaValue.Layout.Column = 1;
240 app.SurfaceAreaValue.Text = sprintf('表面积: %.3f m²', calculateSurfaceArea(app, app.DefaultRadius, calculateHeight(app, app.DefaultRadius)));
241
242 % 创建最优解按钮
243 app.OptimalButton = uibutton(controlGrid);
244 app.OptimalButton.Layout.Row = 6;
245 app.OptimalButton.Layout.Column = 1;
246 app.OptimalButton.Text = '显示最优解';
247 app.OptimalButton.ButtonPushedFcn = @(s,e) OptimalButtonPushed(app, e);
248
249 % 创建图表显示区域
250 app.PlotAxes = uiaxes(app.RightPanel);
251 app.PlotAxes.Position = [50 50 500 500];
252 end
253 end
254
255 % App creation and startup functions
256 methods (Access = public)
257 % 创建UIFigure和组件
258 function createUIFigure(app)
259 createComponents(app)
260
261 % 显示UI
262 app.UIFigure.Visible = 'on';
263 end
264 end
265
266 % Component initialization
267 methods (Access = private)
268 % 初始化App
269 function startupFcn(app)
270 updateContainer(app)
271 updatePlot(app)
272 end
273 end
274
275 % App creation and startup functions
276 methods (Access = public)
277 % 构造函数
278 function app = BucketOptApp
279 % 创建UIFigure和组件
280 createUIFigure(app)
281
282 % 运行startup函数
283 startupFcn(app)
284 end
285 end
286end
模型的碎碎念
这么简单的问题,为什么要纠结?通过这个例子,我们可以窥见目前科学和工程技术研究中解决问题的基本思路:建模。
模型:如果研究者$B$用对象$A^*$来解决对象$A$的某个问题,则称$A^*$为$A$的模型。
这里的定义是一个一般的形式定义,使用的也是一般的用语。这里面,研究者$B$就是建模的主体,而某个问题就是特指的特定问题,而非是泛化的问题,通常是分析、设计、控制、优化等。
而关于系统$A$的模型$A^*$,则挺有意思的。
- 模型$A^*$是关于系统$A$仅仅对解决特定问题有用的简化描述;
- 模型并非总是越复杂越好,恰恰相反,最佳模型是1)符合目的(解决问题)的2)最简单模型;
- 简化是建立模型的基本手段;
- 解决具体问题,总是从最简单的模型出发,逐步增加复杂度,直到模型满足解决该问题的要求。
通常,会采用一个称为$\{S,Q,M\}$的元组来描述一个模型,其中$S$是系统,$Q$是问题,$M$是数学描述。
$$ A^* = \{S, Q, M\} $$对我们上面的对象,毫无疑问,$Q$是一个优化问题,也就是$Q=\arg\min_{S_p} \quad A$。而这里$S$的数值表达形式:$S_p$,包含了简化的描述系统$S$的参数,也就是$S_p=\{r,h\}$。
而$M$,则是$S$和$Q$的数学描述,也就是$M=\{V,A\}$。
$$ M=\{V,A\} $$那么对于简单的优化问题,我们可以采用上面的符号推导的方式来进行求解,对于问题中的约束条件,则可以采用拉格朗日乘子法来进行求解。
对于更加复杂($S$复杂、$Q$复杂、$M$复杂或者多个条件复杂)的问题,则需要采用更加复杂的优化算法,比如牛顿法、拟牛顿法、共轭梯度法、内点法、外点法等经典方法;或者采用智能优化算法,比如遗传算法、粒子群算法等。
文章标签
|-->matlab |-->symbolic |-->Lagrange multiplier |-->syms |-->assume |-->diff |-->subs |-->solve |-->assert |-->pretty |-->vpa
- 本站总访问量:loading次
- 本站总访客数:loading人
- 可通过邮件联系作者:Email大福
- 也可以访问技术博客:大福是小强
- 也可以在知乎搞抽象:知乎-大福
- Comments, requests, and/or opinions go to: Github Repository
