用Matlab实现全局灵敏度Sobol指标计算
什么叫灵敏度
灵敏度分析是研究与分析一个系统（数学模型）输入参数的变动对其输出结果的影响程度的方法。
对于一个函数：
$$ y = f(x_1, x_2, \cdots, x_n) $$如果输入参数 $x_1$ 变化了 $\Delta x_1$，那么输出 $y$ 的变化量 $\Delta y$ 可以表示为：
$$ \Delta y = \frac{\partial f}{\partial x_1} \Delta x_1 $$这个表征的是在某个局部点，输入参数 $x_1$ 变化了 $\Delta x_1$，输出 $y$ 的变化量 $\Delta y$。
也成为局部灵敏度。与之对应，对一个不能抽象为无穷小的有限区域中，输入参数的变化对输出参数的变化的影响，称之为全局灵敏度。全局灵敏度有有很多种表示方法，最为常见的是 Sobol 指标。
Sobol 指标
Sobol指标是基于variance（方差）的指标。对于前面的函数，把输入的参数
$$ X = (x_1, x_2, \cdots, x_n) $$当做一个随机向量，根据输入变量的方差和输出变量的方差来描述输入变量对输出变量的贡献程度。
因此上面的函数写为随机变量的形式：
$$ Y = f(X) $$这里实际上核心要处理的问题就是$n$为变量之间的组合和相关性的问题。对于$1,\ldots, n$的任意子集合$I \subseteq \{1,\ldots, n\}$，定义：
$$ X_I = (x_i)_{i \in I} $$可以把$Y$的方差表达为$X$的函数。
$$ \text{Var}(Y) = \sum_{I \subseteq \{1,\ldots, n\}} V_I \tag{1} $$这里的$V_I$表示的是$I$的所有子集合给$Y$带来的方差。
$$ V_I = \text{Var}\left[ \sum_{J \subseteq I} (-1)^{|I|-|J|} \mathbb{E}[Y | X_J] \right] \tag{2} $$这个公式非常抽象，但是理解下意思就行了。我们可以从1、2个变量的集合来理解。$\hat{V}_i$ 表示的是变量 $x_i$ 对 $Y$ 的贡献，$\hat{V}_{ij}$ 表示的是变量 $x_i$ 和 $x_j$ 对 $Y$ 的联合贡献。
对于 $1 \le i, j \le n$，定义$\hat{V}_i = V_{\{i\}}$，$\hat{V}_{ij} = V_{\{i,j\}}$。
$$ \hat{V}_i = \text{Var}\left[\mathbb{E}[Y | X_i]\right] $$$$ \begin{aligned} \hat{V}_{ij} & = \text{Var}\left[\mathbb{E}[Y | X_i, X_j]\right] - \mathbb{E}[Y|X_i] - \mathbb{E}[Y|X_j] \\ & = \text{Var}\left[\mathbb{E}[Y | X_i, X_j]\right] - \hat{V}_i - \hat{V}_j \end{aligned} $$所以$Y$的方差可以写为如下：
$$ \text{Var}(Y) = \sum_{i=1}^n \hat{V}_i + \sum_{1 \le i < j \le n} \hat{V}_{ij} + \cdots + \hat{V}_{1,2,\cdots, n} \tag{3} $$因为有式(1)，可以把式(3)写为：
$$ \sum_{i=1}^n S_i + \sum_{1 \le i < j \le n} S_{i, j} + \cdots + S_{1,2,\cdots, n} = 1 \tag{4} $$这里的$S_i = \hat{V}_i / \text{Var}(Y)$表示的是变量$x_i$对$Y$的贡献，$S_{i, j} = \hat{V}_{ij} / \text{Var}(Y)$表示的是变量$x_i$和$x_j$对$Y$的联合贡献。
在这些概念的基础上，可以定义全排列Sobol指标，首先定义
$$ VT_i = \sum_{I, i\in I} V_I, V_{-i} = \text{Var}\left[ \mathbb{E}[Y | X_1, \ldots, X_{i-1}, X_{i+1}, \ldots, X_n] \right] \tag{5} $$这里$VT_i$是对所有包含$x_i$的子集合的$V_I$的求和，$V_{-i}$是对所有不包含$x_i$的子集合的$V_I$的求和。说来说去，就是为了把所有包含$x_i$的子集合的$V_I$的求和，和所有不包含$x_i$的子集合的$V_I$的求和分开。在此基础上定义，全排列Sobol指标：
$$ ST_i = VT_i / \text{Var}(Y) = 1 - V_{-i} / \text{Var}(Y) \tag{6} $$下面的两个图就显示了$S_i$的含义，也就是$x_i$对$Y$的单独贡献，排除了其他变量的影响。。对于两个变量的情况，非常容易理解。
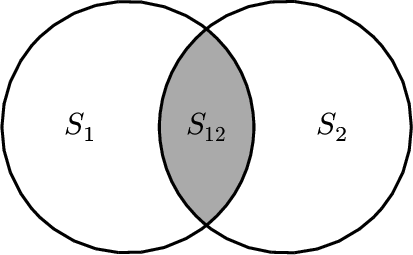
三个变量的情况，也很类似，就是相互交叉的影响一下子增加了很多。
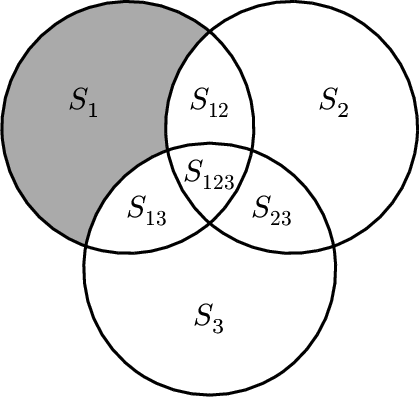而下图就显示了$ST_i$的含义。也就是$x_i$对$Y$的全部贡献，包含了其他变量的交互影响。
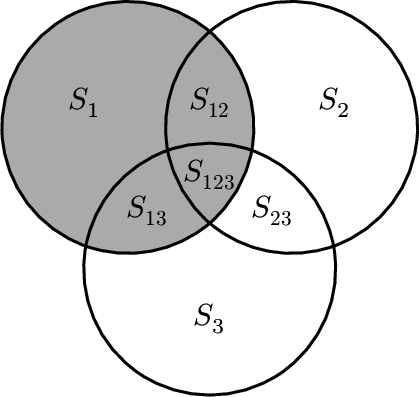
计算方法
那这个玩意怎么算？
就先整一个最简单的例子：
$$ y = x_1 + x_2 + x_3, \quad x_1, x_2, x_3 \in [0, 1] $$我们随便拍个脑袋，就能差不多猜到，
$$ \begin{aligned} S_1 = ST_1 & = \frac{1}{3} \\ S_2 = ST_2 & = \frac{1}{3} \\ S_3 = ST_3 & = \frac{1}{3} \\ S_{1,2} & = 0 \\ S_{1,3} & = 0 \\ S_{2,3} & = 0 \\ S_{1,2,3} & = 0 \\ \end{aligned} $$如果我们采用QMC，应该怎么计算呢？
首先，我们有：
$$ \bar{y} = \frac{1}{N} \sum_{i=1}^N f(x_i) $$$$ \text{Var}(y) = \frac{1}{N} \sum_{i=1}^N f(x_i)^2 - \bar{y}^2 $$这两个是非常容易计算的，只需要对$x_i, i=1,2,3$进行采样，然后计算$f(x_i)$，然后计算$\bar{y}$和$\text{Var}(y)$。
1f = @(x) x(:,1) + x(:,2) + x(:,3);
2bar_y = @(n) mean(f(rand(n, 3)));
3var_y = @(n) mean(f(rand(n, 3)) .^ 2) - bar_y(n) ^ 2;
那么，对应的Sobol指标计算实际上要做两次采样，两次采样对应的样本中，有一个变量（列）是相同的，其他变量是随机的，写成代码大概就是这样的。
$$ \hat{V}_i + \bar{y}^2 = \frac{1}{N} \sum_{i=1}^N f(x_i^1) f(x_i^2) = \overline{y^2}_i $$ 1function S_i = sobol_i(f, N, n, i)
2% f: 函数
3% N: 采样点数
4% n: 变量数
5% i: 变量索引
6
7% 第一次采样
8sample_1 = rand(N, n);
9
10% 第二次采样
11idx = 1:n;
12sample_2 = sample_1;
13sample_2(:, idx(idx~=i)) = rand(N, n-1);
14
15% 计算第一次采样的均值
16hat_f_0 = mean(f(sample_1));
17
18% 计算第一次采样的方差
19D = mean(f(sample_1) .^ 2) - hat_f_0 ^ 2;
20
21% 计算积分值
22D_i = mean(f(sample_1) .* f(sample_2)) - hat_f_0 ^ 2;
23
24S_i = D_i / D;
对于2阶的Sobol指标，也可以通过两次采样完成，这里的两列在两个样本中保持不变，其他列进行两次采样。
$$ \hat{V}_{ij} + \hat{V}_i + \hat{V}_j + \bar{y}^2 = \frac{1}{N} \sum_{i=1}^N f(x_{i,j}^1) f(x_{i,j}^2) = \overline{y^2}_{i,j} $$更高阶的Sobol指标，也可以通过多次采样完成，参照式(2)逐步得到。因为，这里是按照方差来计算，所以，最多进行两次重采样，每次固定要求对应Sobol指标的列，其他列进行随机采样，根据两次采样的$x$值，计算出对应的$y$值，按照
$$ \overline{y^2}_{i,j, k, \ldots, l} = \frac{1}{N} \sum_{i=1}^N f(x_{i,j, k, \ldots, l}^1) f(x_{i,j, k, \ldots, l}^2) $$这里的$x_{i,j, k, \ldots, l}^1$和$x_{i,j, k, \ldots, l}^2$是两次采样的结果，其中$i,j, k, \ldots, l$列在两次采样中保持不变（即只采样一次）。
$$ \hat{V}_{i,j,k} - \hat{V}_{i,j} - \hat{V}_{i,k} - \hat{V}_{j,k} + \hat{V}_{i} + \hat{V}_{j} + \hat{V}_{k} + \bar{y}^2 = \overline{y^2}_{i,j,k} $$联立起来可以得到一个最终的公式：
$$ \begin{aligned} \hat{V}_i &= \overline{y^2}_i - \bar{y}^2 \\ \hat{V}_{ij} &= \overline{y^2}_{ij} - \overline{y^2}_i - \overline{y^2}_j + \bar{y}^2 \\ \hat{V}_{ijk} &= \overline{y^2}_{ijk} - \overline{y^2}_{ij} - \overline{y^2}_{ik} - \overline{y^2}_{jk} + \overline{y^2}_i + \overline{y^2}_j + \overline{y^2}_k - \bar{y}^2\\ \hat{V}_{i,j,k, l} &= \overline{y^2}_{i,j,k,l} - \sum_{I_3 = C_{i,j,k,l}^3}\overline{y^2}_{I_3} + \sum_{I_2 = C_{i,j,k,l}^2}\overline{y^2}_{I_2} - \sum_{I_1 = C_{i,j,k,l}^1}\overline{y^2}_{I_1} + \bar{y}^2 \\ \end{aligned} $$在$\hat{V}_I$的基础上，可以计算出$S_I$和$ST_I$。
最基本的还是把积分转化为求和的Monte Carlo的基本思想。
感想
涉及到概率的东西还是那么难……淦！
对了，那三个图用Typst画的。
编译后就能得到pdf文件，用ImageMagick转换为png文件，然后插入到Typst中。
1typst compile venn2.typ
2typst compile venn3.typ
3typst compile venn3_2.typ
1convert -density 200 venn2.pdf -quality 100 venn2.png
2convert -density 200 venn3.pdf -quality 100 venn3.png
3convert -density 200 venn3_2.pdf -quality 100 venn3_2.png
还挺好看的。
文章标签
|-->matlab |-->全局灵敏度 |-->Sobol指标 |-->蒙特卡洛 |-->Monte Carlo |-->Quasi Monte Carlo
- 本站总访问量：次
- 本站总访客数：人
- 可通过邮件联系作者：Email大福
- 也可以访问技术博客：大福是小强
- 也可以在知乎搞抽象：知乎-大福
- Comments, requests, and/or opinions go to: Github Repository
