2024-11-14 |欢迎您，第位读者！|

Geometry_Function_In_Matlab中描述PDE积分区域的函数法

几何函数

如何描述一个2D的几何形状？如何描述偏微分方程求解中所涉及的2D几何区域？

偏微分方程定义域

这个几何形状是PDE求解的区域。也就是说偏微分方程这个区域中取值（初始值和状态值、系数），在区域的边界上设定边界条件。

$$ m \frac{\partial^2 u}{\partial t^2} + d \frac{\partial u}{ \partial t} - \nabla \cdot (c \nabla u) + a u = f $$

或者，方程组

$$ \mathbf{m} \frac{\partial^2 \mathbf{u}}{\partial t^2} + \mathbf{d} \frac{\partial\mathbf{u}}{\partial t} - \nabla \cdot (\mathbf{c} \otimes \nabla \mathbf{u}) + \mathbf{a} \mathbf{u} = \mathbf{f} $$

在区域中进行考虑，准确的说是方程中的变量$u$、$\mathbf{u}$定义在区域上，所以$\nabla$也在区域的两个坐标$x, y$上定义。

$$ \nabla = \left[\frac{\partial}{\partial x}, \frac{\partial}{\partial y}\right]^\text{T} $$

根据偏微分方程的特性，只有单联通区域中的值才会相互影响，这就为描述区域提供了一些约束，这些约束可以大大简化积分区域的描述。

区域的假设与推论

2D区域是互不相交的单联通区域的并集 $\mathbb{D}$
不失一般性，假设$\mathbb{D}$为单个单联通区域
一个单联通区域可能把整个的 $\mathbb{R}^2$ 分割为 $n+1$个单联通子区域 $\{D_i\}$，$i=0,1,2,\ldots, n$，不失一般性假设$D_0=\mathbb{D}$
一个单联通区域有若干闭环边界$\{\Omega_i\}$，$i=1,2,\ldots, n$
进一步，可设$D_0$的外边界对应$\Omega_1$，且$D_1, D_2, \ldots, D_n$为互不相交单联通区域，且

$$ \mathbb{D} = D_0 - D_1 - D_2 - \ldots - D_n $$

这样，我们就把这个2D几何区域简化成一个单联通的区域，这个单联通区域中可能挖去了0个或者若干个单联通区域。只有一阶嵌套。

所以，问题简化为，如何描述一个闭环边界$\Omega$包围的单联通区域$D$？

描述函数

通用讨论

要描述这样的一个区域，跟描述其闭环边界是同一个意思。$xy$平面的曲线，写成参数方程就是$\left(x(t), y(t)\right)$，还能对$t$有一些约束条件，比如$t \propto s$，这里$s$为曲线的长度坐标。

这是显式的方法，当然还有隐式的方法，比如

$$ a^2x^2 + b^2y^2 = 1 $$

就是一个椭圆曲线。

其实还有一种描述方法就是距离函数，signed distance function。

将区域的内部定义为正向，区域的外部定义为负向，把平面上一个点到曲线的最近距离定义为函数的值：

$$ \theta(x, y) = \begin{cases} - d_{min} & x, y \text{ outside} \\ 0 & x,y\text{ on curve} \\ d_{min} & x,y\text{ inside} \end{cases} $$

这个描述也有一些很好玩的特性。

Matlab PDE工具箱的实现

Matlab PDE工具箱的fegeometry可以用一个函数句柄（称为几何函数）来描述2D形状，对这个函数，Matlab进行了如下的约定：

每一个闭合曲线/区域（称为区域），用至少两个曲线（称为边）来描述，这个曲线集合中的曲线，仅仅能在头、尾除相连；
根据输入参数的个数，函数范围相关的信息来描述区域

几何函数的范围值定义如下：

0个输入参数n=geomFunc;：返回边的条数
1个输入参数d=geomFunc(bs);：输入为一个数组（长度为$n$），边的编号，返回一个矩阵$4\times n$，每列（4行）代表一个边，起点的参数$t_0$，终点的参数$t_1$，左边区域的标签，右边区域的标签。这里的区域标签就对应着子区域的编号，约定，区域外部的编号为0
2个输入参数[x,y]=geomFunc(bs, s);：这里的s就代表曲线长度的数组（长度为$n$），bs对应为边，可以是一个标量（这个标量会广播到每一个s），也可以是一个长度为$n$的向量，程序返回对应点的坐标x和y。

这里唯一有意思的就是左边和右边的定义问题。按照曲线参数方程的定义，一个曲线

$$ [x(t),y(t)]^{\text{T}}, t\in [0, s] $$

按照参数增长的方向，前进的左边和右边就是这里定义的左和右。因此，曲线的起点和终点的定义是最终影响左、和右的关键。

例子

上面的定义很清楚，那么下面就是例子。第一个例子当然是Matlab自带的一个例子，就是一个圆。

1edit circleg

就能看到这个函数的源代码。

 1function [x,y]=circleg(bs,s)
 2nbs=4; % Number of boundary segments
 3
 4d=[0 0 0 0   % Start parameter value
 5   1 1 1 1   % End parameter value
 6   1 1 1 1   % Left hand region
 7   0 0 0 0]; % Right hand region
 8
 9start_angles = [0;pi/2;pi;3*pi/2];
10switch nargin
11    case 0
12        x=nbs; 
13    case 1    
14        x=d(:,bs);
15    case 2
16        if isscalar(bs)
17            bs = repmat(bs,size(s));
18        end
19        x = zeros(size(s));
20        y = zeros(size(s));
21        for i = 1:numel(s)
22           segment = bs(i);
23           offset = pi/2*s(i);
24           angle = start_angles(segment)+offset;
25           x(i) = cos(angle);
26           y(i) = sin(angle);            
27        end
28end

这里，很容易可以反推出：

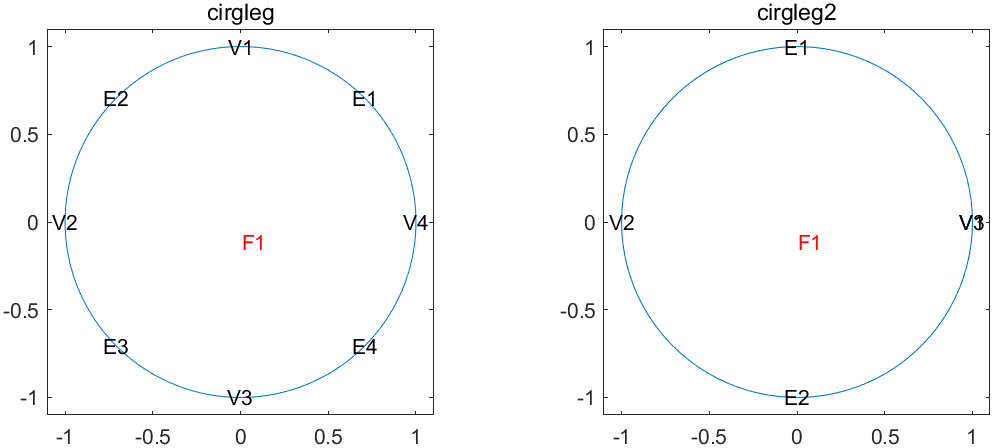
由四条曲线来描述一个圆；
每个曲线的参数范围都是从0到1，曲线左边为内部区域，右边为外部区域
这里还用了数组bs作为坐标来索引d矩阵
最后，在计算坐标位置时，可以看到，四个曲线的起点分别为0,pi/2,pi和 3pi/2,然后，每个去线段的长度对应弧度pi/2。

那么，如果我们要用两个曲线来描述一个圆，会是什么样的呢？

 1function [x,y]=circleg2(bs,s)
 2
 3nbs=2; % Number of boundary segments
 4
 5d=[0 0   % Start parameter value
 6    1 1   % End parameter value
 7    1 1   % Left hand region
 8    0 0]; % Right hand region
 9
10start_angles = [0;pi];
11switch nargin
12    case 0
13        x=nbs;
14    case 1
15        x=d(:,bs);
16    case 2
17        if isscalar(bs)
18            bs = repmat(bs,size(s));
19        end
20        x = zeros(size(s));
21        y = zeros(size(s));
22        for i = 1:numel(s)
23            segment = bs(i);
24            offset = pi*s(i);
25            angle = start_angles(segment)+offset;
26            x(i) = cos(angle);
27            y(i) = sin(angle);
28        end
29end

调用下面的函数输出区域：

结果输出代码：

 1tiledlayout(1, 2);
 2
 3nexttile;
 4pdegplot(@circleg,"EdgeLabels","on","FaceLabels","on", "VertexLabels", "on");
 5set(gca, 'XLim', [-1.1, 1.1], 'YLim', [-1.1, 1.1]); 
 6title('cirgleg');
 7
 8nexttile;
 9pdegplot(@circleg2,"EdgeLabels","on","FaceLabels","on", "VertexLabels", "on");
10set(gca, 'XLim', [-1.1, 1.1], 'YLim', [-1.1, 1.1]); 
11title('cirgleg2');
12
13exportgraphics(gcf, 'circleg.png')

 1>> fegeometry(@circleg)
 2
 3ans = 
 4
 5  fegeometry - 属性:
 6
 7       NumFaces: 1
 8       NumEdges: 4
 9    NumVertices: 4
10       NumCells: 0
11       Vertices: [4x2 double]
12           Mesh: []
13
14
15>> fegeometry(@circleg2)
16
17ans = 
18
19  fegeometry - 属性:
20
21       NumFaces: 1
22       NumEdges: 2
23    NumVertices: 3
24       NumCells: 0
25       Vertices: [3x2 double]
26           Mesh: []

这两个函数产生的几何体，区别就在于边的条数和节点的个数：

4条曲线，对应4个边，4个端点
2条曲线，对应2条边，3个端点

我不是很理解的是为什么，4条曲线时，进行了正确的端点合并，而2条曲线时，端点没有正确合并？

 1>> fegeometry(@circleg2).Vertices
 2
 3ans =
 4
 5    1.0000         0
 6   -1.0000    0.0000
 7    1.0000   -0.0000
 8
 9
10>> fegeometry(@circleg).Vertices
11
12ans =
13
14    0.0000    1.0000
15   -1.0000    0.0000
16   -0.0000   -1.0000
17    1.0000   -0.0000

会影响网格吗？

 1tiledlayout(1,2);
 2
 3nexttile;
 4pdeplot(generateMesh(fegeometry(@circleg)).Mesh);
 5title('circleg');
 6
 7nexttile;
 8pdeplot(generateMesh(fegeometry(@circleg2)).Mesh);
 9title('circleg2'); 
10
11exportgraphics(gcf, 'circleg-circleg2.png')

看起来没有什么影响。

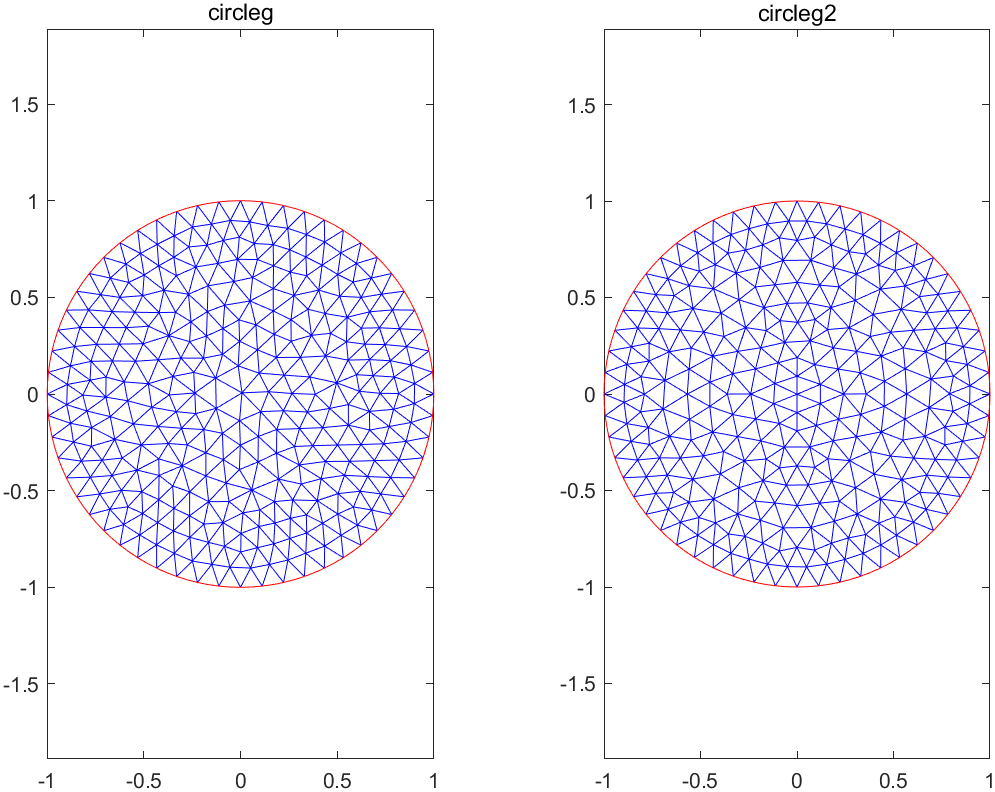
当然，还是有一个影响，就是在设定元素的网格尺寸时，过少的边会减少设定的精确性，所以在建立几何条件是，应该充分考虑网格加密的设定问题。

 1tiledlayout(2,2)
 2nexttile;
 3g = generateMesh(fegeometry(@circleg2), 'Hvertex', {[1], 0.01})
 4pdeplot(g.Mesh);
 5title('circleg2');
 6nexttile;
 7g = generateMesh(fegeometry(@circleg2), 'Hvertex', {[2], 0.01})
 8pdeplot(g.Mesh);
 9title('circleg2');
10nexttile;
11g = generateMesh(fegeometry(@circleg2), 'Hvertex', {[3], 0.01})
12pdeplot(g.Mesh);
13title('circleg2');
14
15nexttile;
16g = generateMesh(fegeometry(@circleg2), 'Hedge', {[1], 0.01})
17pdeplot(g.Mesh);
18title('circleg2');

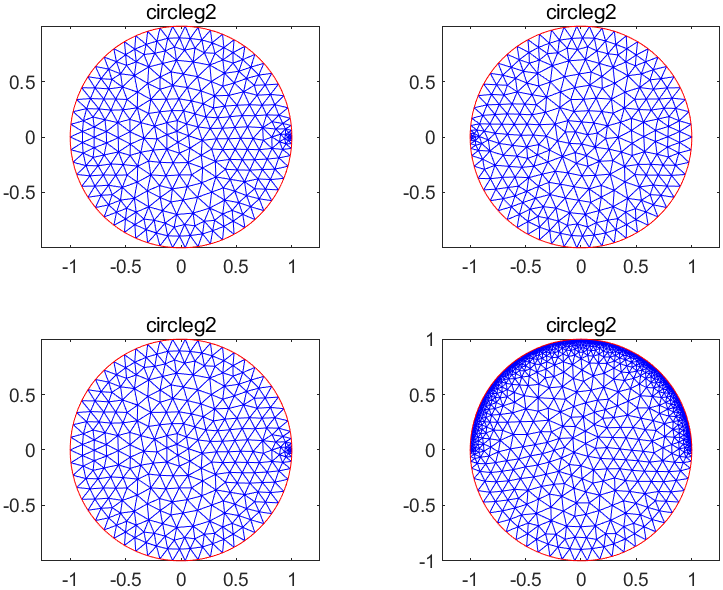
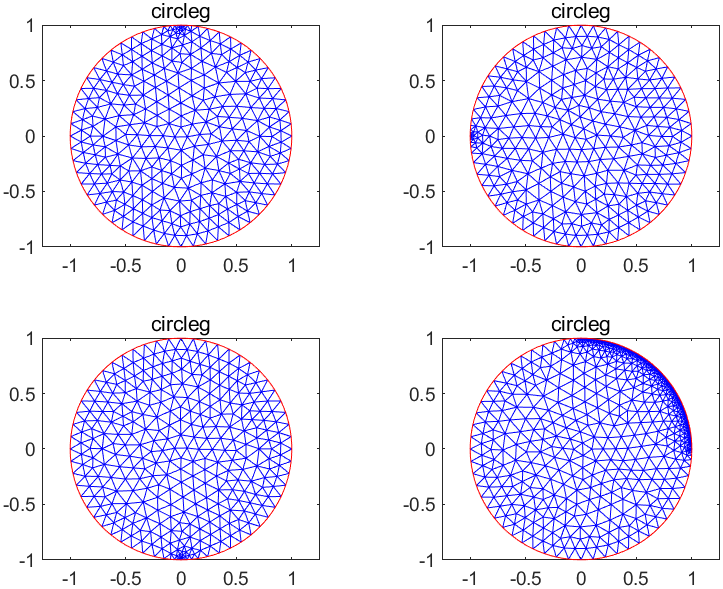
可以看到，在进行加密时，这两个点没有正确归并并没有影响。同时，更多的边能够提供更好的网格加密控制力度，比如这里，就只能对单个边进行加密，而采用circleg函数的4边描述法，还能够更加精细地控制加密区域。

 1tiledlayout(2,2)
 2nexttile;
 3g = generateMesh(fegeometry(@circleg), 'Hvertex', {[1], 0.01})
 4pdeplot(g.Mesh);
 5title('circleg');
 6nexttile;
 7g = generateMesh(fegeometry(@circleg), 'Hvertex', {[2], 0.01})
 8pdeplot(g.Mesh);
 9title('circleg');
10nexttile;
11g = generateMesh(fegeometry(@circleg), 'Hvertex', {[3], 0.01})
12pdeplot(g.Mesh);
13title('circleg');
14
15nexttile;
16g = generateMesh(fegeometry(@circleg), 'Hedge', {[1], 0.01})
17pdeplot(g.Mesh);
18title('circleg');

总结

Matlab PDE工具箱约定了一个显式描述积分区域的方法。上面介绍了基本的单边界单联通简单区域的函数定义方法，并简单探讨了对网格生成的影响。