2024-10-17 |欢迎您，第位读者！|

Thermal_Transient_in_Matlab统一偏微分框架之热传导问题

固体热传导方程

固体热传导的方程为：

$$ \rho C_p \left( \frac{\partial T}{\partial t} + \mathbf{u}_{\mathtt{trans}} \cdot \nabla T \right) + \nabla \cdot (\mathbf{q}+\mathbf{q}_r) = -\alpha T \frac{d \mathbf{S}}{dt} + \mathbf{Q} $$

这里涉及的参数包括：

参数	含义
$\rho$	密度， $\mathtt{kg}/\mathtt{m}^3$
$C_p$	比热容， $\mathtt{J}/\mathtt{kg} \cdot \mathtt{K}$
$T$	温度， $\mathtt{K}$
$\mathbf{u}_{\mathtt{trans}}$	位移速度， $\mathtt{m}/\mathtt{s}$
$\mathbf{q}$	热流密度， $\mathtt{W}/\mathtt{m}^2$
$\mathbf{q}_r$	辐射热流密度， $\mathtt{W}/\mathtt{m}^2$
$\alpha$	热膨胀系数， $\mathtt{K}^{-1}$
$\mathbf{S}$	第二Piola-Kirchhoff 应力张量， $\mathtt{Pa}$
$\mathbf{Q}$	额外的热源， $\mathtt{W}/\mathtt{m}^3$

将内部热传导的热流简化为传热系数与温差的乘积：

$$ \mathbf{q} = -k \nabla T $$

这里的$k$是热传导系数，单位是 $\mathtt{W}/\mathtt{m} \cdot \mathtt{K}$。

忽略热辐射、运动和应力张量等项，上述方程可以简化为：

$$ \rho C_p \frac{\partial T}{\partial t} - \nabla \cdot (k \nabla T) = Q $$

通常只需要考虑以下量值：

参数	含义
$t$	时间自变量
$\mathbf{x}$	空间自变量
$T$	温度，传热方程积分应变量
$Q$	热源，抽象为（通常是边界）单元的热载荷
$\rho$	密度，物性，基本不随温度变化
$k$	热传导系数，物性，随温度变化
$C_p$	比热容，物性，随温度变化

定义热扩散系数为

$$ \alpha = \frac{k}{\rho C_p} $$

积分传热方程时，可以考虑把对应的参数都设为1，此时，方程变为：

$$ \frac{\partial T}{\partial t^*} - \nabla \cdot \nabla T = Q/k $$

这里的$t^*$是无量纲时间，定义为：

$$ t^* = \alpha t $$

有限元求解过程

对中间有一个空洞的矩形区域，求解其热传导方程。

通过CSG建模，生成一个矩形区域，然后在中间挖去一个小矩形区域。先建一个函数：

1function gg = blockWithCavity
2
3rect1 = [3 4 -0.5 0.5 0.5 -0.5 0.8 0.8 -0.8 -0.8];
4rect2 = [3 4 -0.1 0.1 0.1 -0.1 0.4 0.4 -0.4 -0.4];
5gd = [rect1', rect2'];
6sf = 'R1 - R2';
7ns = char('R1', 'R2')';
8
9gg = decsg(gd, sf, ns);

然后在计算程序中调用这个函数产生几何体。

1%% model and geometry
2g = blockWithCavity;
3model = femodel(AnalysisType="thermalTransient",...
4    Geometry=g);
5
6h = figure(1);
7pdegplot(model,EdgeLabels="on");
8xlim([-0.6,0.6])
9ylim([-1,1])

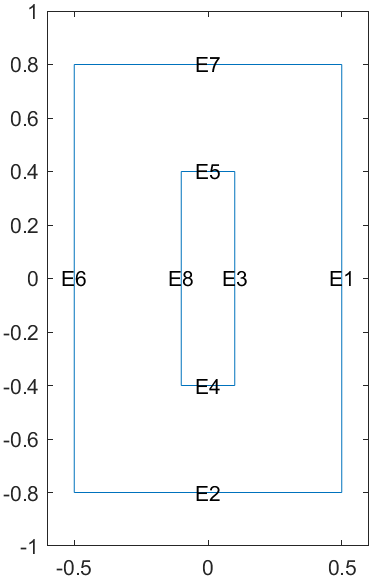
blockWithCavity

按照前面说所说的，把参数都设为1，这样得到解，只会有时间尺度上的线性差异。

1model.MaterialProperties = ...
2            materialProperties(ThermalConductivity=1, ...
3                               MassDensity=1, ...
4                               SpecificHeat=1);

边界同样和初始条件（因为是时变问题）在程序中设定：

1%% boundary conditions and initial conditions
2
3model.EdgeBC(6) = edgeBC(Temperature=100);
4model.EdgeLoad(1) = edgeLoad(Heat=-10);
5
6model.FaceIC = faceIC(Temperature=-10);

采取默认的网格：

1%%
2model = generateMesh(model);
3
4figure(2);
5pdemesh(model);
6title("Mesh with Quadratic Triangular Elements")
7xlim([-0.6,0.6])
8ylim([-1,1])

mesh

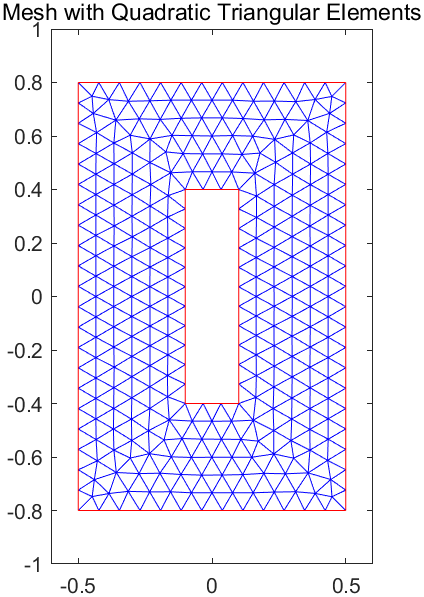
最后，调用fesolve函数求解：

1%%
2
3tlist = 0:.1:5.0;
4results = solve(model,tlist)

results语句后面没有分号，直接显示得到的结果：

results = 

  TransientThermalResults - 属性:

      Temperature: [1232×51 double]
    SolutionTimes: [0 0.1000 0.2000 0.3000 0.4000 0.5000 0.6000 0.7000 0.8000 0.9000 1 … ] (1×51 double)
       XGradients: [1232×51 double]
       YGradients: [1232×51 double]
       ZGradients: []
             Mesh: [1×1 FEMesh]

最后就是结果的可视化：

 1[qx,qy] = evaluateHeatFlux(results);
 2
 3figure(3)
 4c = pdeplot(results.Mesh,XYData=results.Temperature(:,end), ...
 5                        Contour="on",...
 6                        FlowData=[qx(:,end),qy(:,end)], ...
 7                        ColorMap="hot");
 8xlim([-0.6,0.6])
 9ylim([-1,1])
10axis equal
11title(sprintf("t = %4.2f", results.SolutionTimes(end)))

mesh

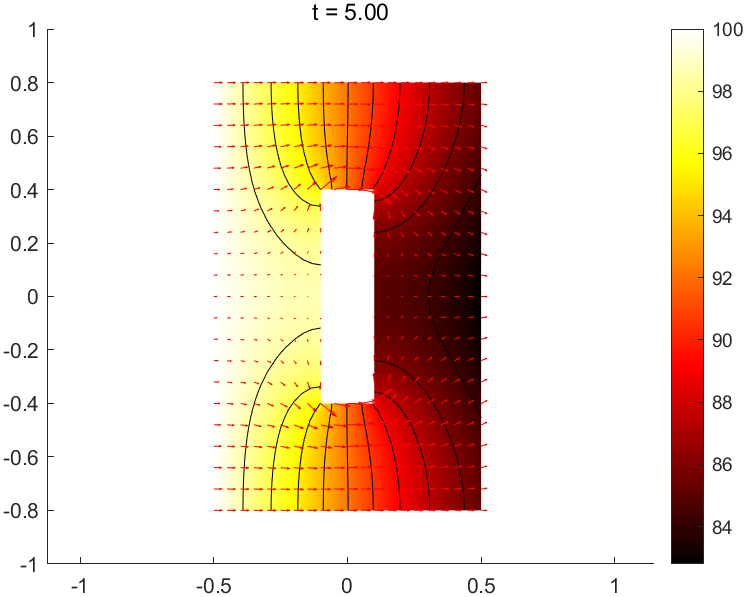
实际上，也很容易利用与前面优化过程可视化相同的方法，将结果可视化成动画。

 1[qx,qy] = evaluateHeatFlux(results);
 2
 3fn = "cavity.gif";
 4if exist(fn, 'file')
 5    delete(fn);
 6end
 7
 8figure(3)
 9
10for i = 1:size(results.Temperature, 2)
11    c = pdeplot(results.Mesh,XYData=results.Temperature(:,i), ...
12                         Contour="on",...
13                         FlowData=[qx(:,i),qy(:,i)], ...
14                         ColorMap="hot");
15    xlim([-0.6,0.6])
16    ylim([-1,1])
17    axis equal
18    title(sprintf("t = %4.2f", results.SolutionTimes(i)))
19    exportgraphics(gca, fn, Resolution=100, Append=true);    
20end

gif

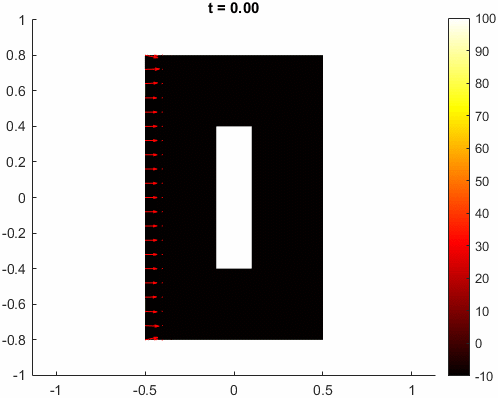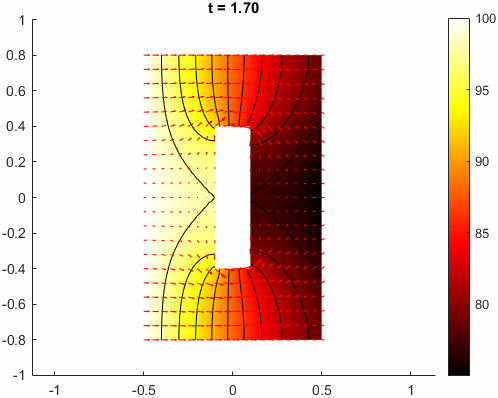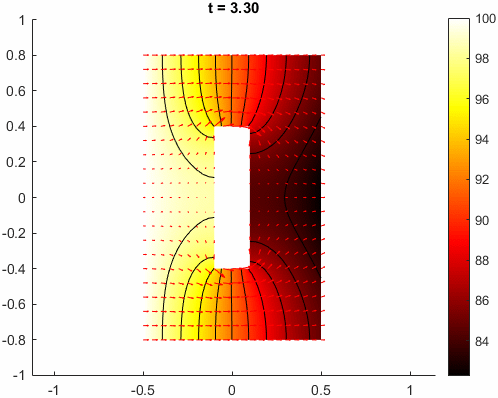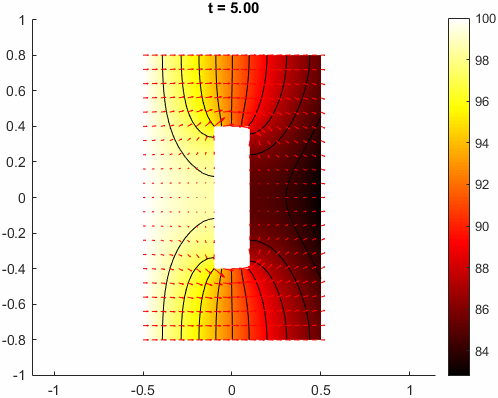
总结

利用统一框架，求解动态热传导方程的过程与求解静力学方程类似，同样是建立模型、设定参数、求解、可视化结果。

不是特别一样的在于，热传导方程的相似参数就只有一个，通过相似性分析，可以简化设定参数的过程，最后结果反应出来的只是时间尺度上的差异。通常而言，$\alpha$ 是一个很小的量，因此传热的过程相对来说是比较慢的，通过无量纲化，计算步长比实际时间要小很多。