Dimensional Analysis量纲分析入门
幂律(Power Law)
$$ y = kx_1^{n_1}x_2^{n_2}\cdots x_m^{n_m} $$其中,$k$ 是常数,$x_1, x_2, \cdots, x_m$ 是变量,$n_1, n_2, \cdots, n_m$ 是幂次。
定理:有单位的物理量,只能形成幂律关系。
这个定理的证明很简单(!)。
证明:不失一般性,假设$y$和$x$是两个有单位的物理量,那么$y$和$x$的关系可以表示为:
$$ y = f(x) $$量纲,也就是物理单位,通常本身也是一种比例关系,例如长度,很原始的基准是手肘到中指尖的长度(英尺),很科幻的现代基准是光在真空中1/299792458秒内走过的距离(米)。有物理单位的量,可以通过取比值的方式来消去单位。
$$ \frac{y_1}{y_2} = \frac{f(x_1)}{f(x_2)} $$这个式子,就是一个与单位无关的公式,也就是说,无论$x$的单位是什么,$y$的单位是什么,这个式子都成立。
那么这里就有一个决定性的推理。
$$ \frac{f(x_1)}{f(x_2)} = \frac{\alpha x_1}{\alpha x_2} $$也就是,$x$取不同的单位,体现为单位转换系数$\alpha$,$\frac{y_1}{y_2}$ 不变。只要这个式子成立,很容易就能得到:$y$和$x$就满足幂律关系。
对上面的式子求取$\alpha$的导数,可以得到:
$$ x_1f(\alpha x_2) f'(\alpha x_1) = x_2 f(\alpha x_1) f'(\alpha x_2) $$对所有的$\alpha, x_1, x_2$,这个式子都成立,我们取$\alpha = 1, x_2 = 1, x_1 = x$,可以得到:
$$ \frac{x f'(x)}{f(x)} = \frac{f'(1)}{f(1)} \equiv k $$这里的$k$是一个常数。
$$ \int \frac{f'(x)}{f(x)} = \int \frac{k}{x} $$计算不定积分,可以得到:
$$ \ln f(x) = k \ln x + c $$取指数,可以得到:
$$ f(x) = C x^k $$这里$C$是另外一个积分常数。Quod Erat Demonstrandum (Q.E.D.)。
当然,从一般的物理规律出发,也能理解为什么有单位的量只能出现在幂律关系中。就比如一个长度量$l$,$e^l$的含义是什么?$\sin(l)$的含义是什么?从数学上来看
$$ e^l = 1 + l + \frac{l^2}{2!} + \frac{l^3}{3!} + \cdots $$等于把无量纲量、长度量、面积量、体积量……全部加在一起,这显然是没有任何物理意义的。
SI量纲
SI量纲,也就是国际单位制,是国际上通用的物理量单位体系。SI量纲有7个基本量,参考国标GB 3100-1993的3.1节SI基本单位:
- 长度($L$), 单位:米($m$)
- 质量($M$), 单位:千克($kg$)
- 时间($T$), 单位:秒($s$)
- 电流($I$), 单位:安培($A$)
- 热力学温度($Θ$), 单位:开尔文($K$)
- 物质的量($N$), 单位:摩尔($mol$)
- 发光强度($J$), 单位:坎德拉($cd$)
我们把一个物理量的单位信息记为$[y]$,表达为上述基本量的幂次形式,例如速度的单位是$\frac{m}{s}$,那么$[v] = L T^{-1}$,加速度的单位是$\frac{m}{s^2}$,那么$[a] = L T^{-2}$。
所以对于有单位物理量$y$,可以表示为:
$$ y = C a^\alpha b^\beta c^\gamma \cdots $$其中$a, b, c, \cdots$是有单位的物理参数,$C$是常数,$\alpha, \beta, \gamma, \cdots$是幂次。
$$ [y] = [a]^\alpha [b]^\beta [c]^\gamma \cdots $$再结合上面的SI量纲,可以得到一组方程,分别对应7个基本量:
$$\begin{split} &[y] = L^{\alpha_y} M^{\beta_y} T^{\gamma_y} I^{\delta_y} Θ^{\epsilon_y} N^{\zeta_y} J^{\eta_y} \\ &[a] = L^{\alpha_a} M^{\beta_a} T^{\gamma_a} I^{\delta_a} Θ^{\epsilon_a} N^{\zeta_a} J^{\eta_a} \\ &[b] = L^{\alpha_b} M^{\beta_b} T^{\gamma_b} I^{\delta_b} Θ^{\epsilon_b} N^{\zeta_b} J^{\eta_b} \\ &[c] = L^{\alpha_c} M^{\beta_c} T^{\gamma_c} I^{\delta_c} Θ^{\epsilon_c} N^{\zeta_c} J^{\eta_c} \\ &\cdots \end{split} $$这样可以得到一组方程:
$$\begin{split} &\alpha_y = \alpha_a \cdot \alpha + \alpha_b \cdot \beta + \alpha_c \cdot \gamma + \cdots \\ &\beta_y = \beta_a \cdot \alpha + \beta_b \cdot \beta + \beta_c \cdot \gamma + \cdots \\ &\gamma_y = \gamma_a \cdot \alpha + \gamma_b \cdot \beta + \gamma_c \cdot \gamma + \cdots \\ &\delta_y = \delta_a \cdot \alpha + \delta_b \cdot \beta + \delta_c \cdot \gamma + \cdots \\ &\epsilon_y = \epsilon_a \cdot \alpha + \epsilon_b \cdot \beta + \epsilon_c \cdot \gamma + \cdots \\ &\zeta_y = \zeta_a \cdot \alpha + \zeta_b \cdot \beta + \zeta_c \cdot \gamma + \cdots \\ &\eta_y = \eta_a \cdot \alpha + \eta_b \cdot \beta + \eta_c \cdot \gamma + \cdots \\ \end{split} $$举个例子
我们来分析一个单摆的周期。单摆的长度为$l$,质量为$m$,角频率为$\omega$,重力加速度为$g$。
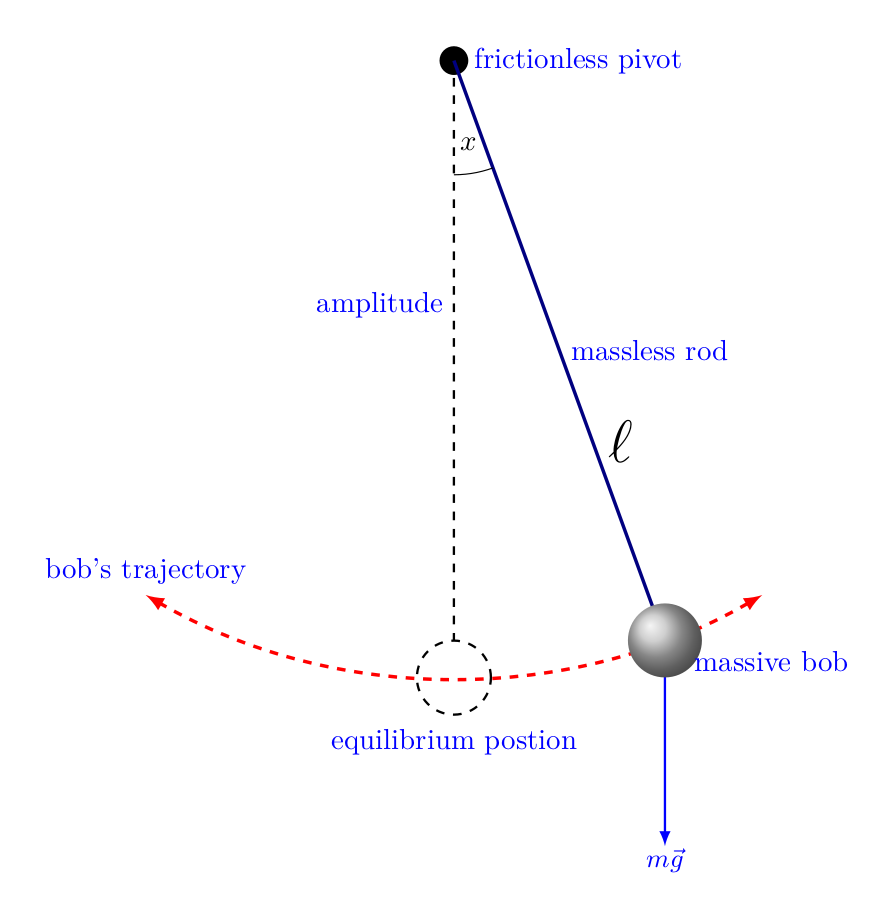
我们写成:
$$ \omega = C l^\alpha m^\beta g^\gamma $$量纲分析有:
$$ \begin{split} &[l] = L \\ &[m] = M \\ &[g] = L T^{-2} \\ &[\omega] = T^{-1} \end{split} $$因此有:
$$ T^{-1} = L^\alpha M^\beta (L T^{-2})^\gamma $$$$\left\{ \begin{split} &\alpha + \gamma = 0 \\ &\beta = 0 \\ & -2\gamma = -1 \end{split} \right. $$解得:
$$ \left\{ \begin{split} &\alpha = -\frac{1}{2} \\ &\beta = 0 \\ &\gamma = \frac{1}{2} \end{split} \right. $$所以有:
$$ \omega = C l^{-\frac{1}{2}} g^{\frac{1}{2}} = C \sqrt{\frac{g}{l}} $$实际上,通过动力学积分,也能够很简单地得到:
$$ \omega = \sqrt{\frac{g}{l}} = 2\pi f $$$$ f = \frac{1}{2\pi} \sqrt{\frac{g}{l}} $$周期为
$$ T = \frac{1}{f} = 2\pi \sqrt{\frac{l}{g}} $$这个很简单的推导就留给读者作为练习(!)。
进一步的讨论
当然,前面的7个方程,其解的情况可以分为三类:
- 无解:这个是时候,我们就知道肯定丢失了重要的参数
- 唯一解:非常幸运,只需要通过实验确定常数$C$
- 多解:依然得到了一些有用的信息,可以用于指导实验
对于无解和唯一解的情形,我们很容易理解。那么对于多解的情形,物理上的含义如何呢?我们如何选择呢?有什么意义呢?
我们再考虑一个例子,用速度$V$把一个质量为$m$的物体向上抛出,这个球所受到的空气阻力服从平方率,也就是阻力$k V^2$。这里的$k$是阻力系数。问,这个物体上升的高度$h$和什么有关?
$$ h = C m^\alpha g^\beta k^\gamma V^\delta $$有$[k] = [force]/[velocity]^2 = M L T^{-2} L^{-2} / (L T^{-1})^2 = M L^{-1}$,所以有:
$$\left\{ \begin{split} & \alpha + \gamma = 0 \\ & \beta - \gamma + \delta = 1\\ & -2\beta -\delta = 0 \end{split} \right. $$这个方程组有无穷多解。例如前面所说的
$$ \left\{ \begin{split} & \alpha = 1 \\ & \beta = 0 \\ & \gamma = -1 \\ & \delta = 0 \end{split} \right. $$这就表明, 上升高度与$m/k$成正比,如果我们把$h$替换为$h/(m/k)$,就可以得到一个无量纲量。进行同样的量纲分析
$$ \frac{h}{m/k} = C m^\alpha g^\beta k^\gamma V^\delta $$得到如下的方程,因为是$h/(m/k)$是无量纲量,所以方程的右边全部是0。
$$\left\{ \begin{split} & \alpha + \gamma = 0 \\ & \beta - \gamma + \delta = 0\\ & -2\beta -\delta = 0 \end{split} \right. $$解得:
$$ \left\{ \begin{split} & \beta = \alpha \\ & \gamma = -\alpha \\ & \delta = -2\alpha \end{split} \right. $$所以有:
$$ \frac{h}{m/k} = C m^\alpha g^\alpha k^{-\alpha} V^{-2\alpha} = C \left(\frac{mg}{k V^2}\right)^\alpha $$从这里我们可以得出结论,$\lambda = \frac{mg}{k V^2}$是我们问题中的唯一需要考虑的无量纲量。
$$ \frac{h}{m/k} = f \left(\frac{mg}{k V^2}\right) \text{, i.e. } h = \frac{m}{k} f \left(\frac{mg}{k V^2}\right) $$因为$\lambda$是一个无量纲量,所以这个函数$f$就不见得是幂律关系。实际上,如果我们简单(!)地分析动力学,可以得到:
$$ f(\lambda) = \frac{1}{2} \ln (1+\lambda ^{-1}) $$推导到这里就有一个问题,因为前面我们选择的组合是随意的,所以的,这个结果有意义吗?这里只是简单展示一下。
例如,
$$\left\{ \begin{split} & \alpha + \gamma = 0 \\ & \beta - \gamma + \delta = 1\\ & -2\beta -\delta = 0 \end{split} \right. $$的解还可能是:
$$ \left\{ \begin{split} & \alpha = 0 \\ & \beta = -1 \\ & \gamma = 0 \\ & \delta = 2 \end{split} \right. $$这个时候,上面的过程就变成了:
$$ \frac{h}{V^2/g} = C m^\alpha g^\beta k^\gamma V^\delta $$当然,这次的量纲方程组求解会得到同样的结果,也就是$\lambda = \frac{mg}{k V^2}$。
$$ h = \frac{V^2}{g} \hat{f} \left(\frac{mg}{k V^2}\right) $$观察发现,
$$ \tilde{f}(\lambda) = \hat{f} / \lambda $$$$ h = \frac{m}{k} \tilde{f} \left(\frac{mg}{k V^2}\right) $$因此,选择不同的解,得到的结果是等价的。
通常,我们也把这个公式写成:
$$ g\left(\frac{mg}{kV^2}, \frac{kh}{m}\right) = 0 $$这里$g$是一个函数,$\frac{mg}{kV^2}$和$\frac{kh}{m}$是两个无量纲量。当然,$g$可以有很多种用$f$表示的形式。
$$ g(x, y) = y - f(x) $$$$ g(x, y) = y^2 - f^2(x) $$或者
$$ g(x, y) = \ln \frac{1+y}{1+f(x)} $$如果在上面的例子里面,我们再增加变量,就是丢球的角度$\theta$,因为$\theta$是角度,一个无量纲量,那么我们就能写成:
$$ h = \frac{m}{k} F \left(\frac{mg}{k V^2}, \theta\right) = \frac{m}{k} F \left(\lambda, \theta\right) $$实际上,$F$无法写出解析形式。
那么,我们这么做有什么意义呢?
通过量纲分析,我们把一个依赖于多个物理量的函数,简化为一个依赖于较少的无量纲量的函数,这非常有助于我们对问题的理解,并且可以指导我们进行实验设计。
抛石问题分析
考虑一个二维的抛石问题,定义位置向量为$\vec{x} = (x, y)$,抛石角度为$\theta$,抛石初速度为$V$。
$$ m \ddot{\vec{x}} = m\vec{g} - k |\dot{\vec{x}}| \dot{\vec{x}} $$展开得到:
$$ \begin{split} & m \ddot{x} = -k \sqrt{\dot{x}^2 + \dot{y}^2} \dot{x} \\ & m \ddot{y} = -k \sqrt{\dot{x}^2 + \dot{y}^2} \dot{y} - mg \end{split} $$$t=0$时,$\vec{x} = (0, 0)$,$\dot{\vec{x}} = (V \cos \theta, V \sin \theta)$。
经过上面的量纲分析,我们可以发现,长度的量纲组合是$m/k$,速度的量纲组合是$V$,那么时间量纲组合是$m/kV$。我们就可以按照量纲组合的把量纲量转化成无量纲量。
$$ X = \frac{x}{m/k}, \quad Y = \frac{y}{m/k}, \quad T = \frac{t}{m/kV} $$根据链式法则,
$$ \dot{x} = \frac{dT}{dt}\frac{dx}{dT} = \frac{kV}{m} \frac{d}{dT}\left(\frac{m}{k} X\right) = V X' $$$$ \ddot{x} = \frac{dT}{dt}\frac{d\dot{x}}{dT} = \frac{kV}{m} \frac{d}{dT}(V X') = \frac{kV^2}{m} X'' $$最终可以得到:
$$ \begin{split} & kV^2 X'' = -k \sqrt{V^2 X'^2 + V^2 Y'^2} V X' \\ & kV^2 Y'' = -k \sqrt{V^2 X'^2 + V^2 Y'^2} V Y' - mg \end{split} $$根据$\lambda = \frac{mg}{kV^2}$,可以得到:
$$ \begin{split} & X'' = - \sqrt{X'^2 + Y'^2} X' \\ & Y'' = - \sqrt{X'^2 + Y'^2} Y' - \lambda \end{split} $$$T = 0$时,$X = 0, Y = 0, X' = \cos \theta, Y' = \sin \theta$。这个方程组的初始值和方程都依赖于无量纲量,整个问题只依赖于两个参数$\lambda$和$\theta$。对于其运动的最高点(对应时间$T_0$),$Y'(T_0) = 0$,此时$h = (m/k) Y(T_0)$。
这就成功地把一个$(m, k, g, V, \theta)$的问题,转化为了一个$(\lambda, \theta)$的求解。我们这里甚至可以给$\lambda$一个名称,考虑到这个参数实际上描述了重力与阻力的相对关系,我们就叫它格拉维-夸德雷特-埃尔雷兹斯唐斯数,简称Grr数。
程序实现
都已经写到这里了,很难不搞一个程序。
1function [value, isterminal, direction] = heightEvent(t, y, Y0)
2% 当Y回到初始高度时停止
3value = y(2) - Y0; % 当前高度与初始高度的差
4isterminal = 1; % 停止积分
5direction = -1; % 只在下降穿过初始高度时停止
6end
7
8function dydt = dimensionlessODE(t, y, lambda)
9% y = [X; Y; X'; Y']
10X = y(1);
11Y = y(2);
12Xp = y(3);
13Yp = y(4);
14
15% Calculate velocity magnitude
16V = sqrt(Xp^2 + Yp^2);
17
18% ODE system
19dydt = zeros(4,1);
20dydt(1) = Xp;
21dydt(2) = Yp;
22dydt(3) = -V * Xp;
23dydt(4) = -V * Yp - lambda;
24end
这两个函数定义了ODE和终止条件(高度再次为0的事件)。
调用ODE45求解,得到结果。
1 function [T, X, Y] = solveDimensionlessODE(app)
2 % 初始条件
3 X0 = 0;
4 Y0 = 0;
5 Xp0 = cos(app.Theta);
6 Yp0 = sin(app.Theta);
7
8 % 求解ODE直到Y回到初始高度
9 y0 = [X0; Y0; Xp0; Yp0];
10 options = odeset('Events', @(t,y) heightEvent(t,y,Y0), ...
11 'RelTol', 1e-8, ... % 相对误差
12 'AbsTol', 1e-8, ... % 绝对误差
13 'MaxStep', 0.01); % 最大步长
14 [T, Y] = ode45(@(t,y) dimensionlessODE(t, y, app.Lambda), [0 100], y0, options);
15
16 X = Y(:,1);
17 Y = Y(:,2);
18 end
界面什么的就不纠结了,左边是几个物理参数:质量、阻力系数、重力加速度、初始速度、抛射角度;下面是相应的参考长度、参考时间、最大投射高度(有量纲、无量纲)。
1app = ProjectileApp;
2exportapp(app.Figure, "mainui.png")
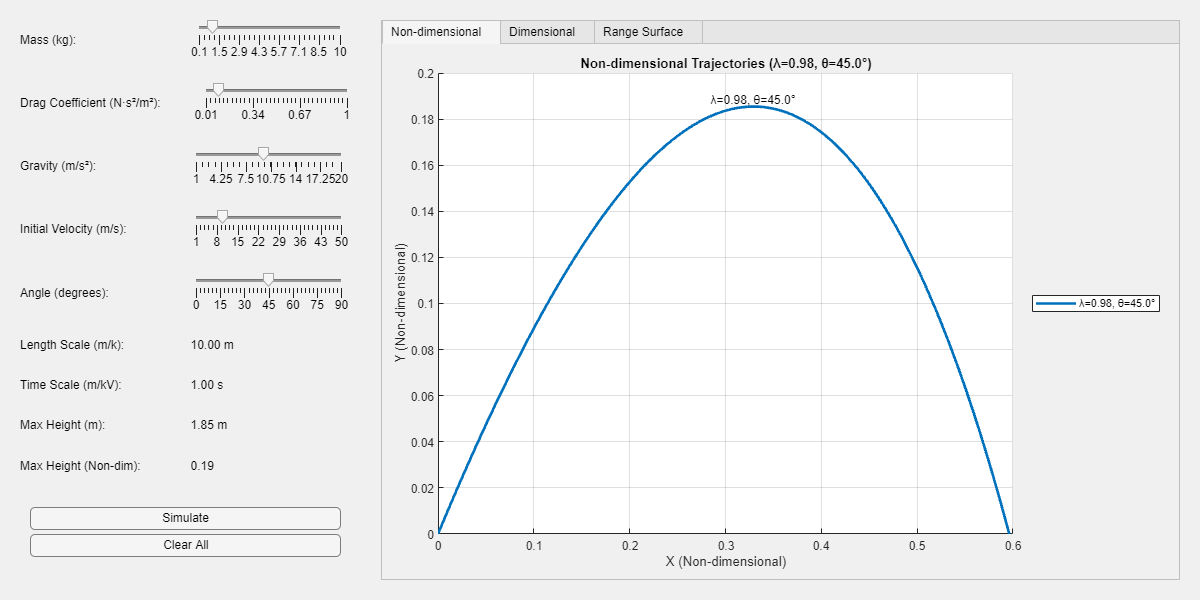
右边两个标签,分别是有量纲的轨迹和两个无量纲参数下最大射程的图形。
我们就演示一个东西,就是不同的质量下的投射距离。我们一通调节质量,得到如下的结果:
1exportgraphics(app.NonDimAxes, "ndt.png")
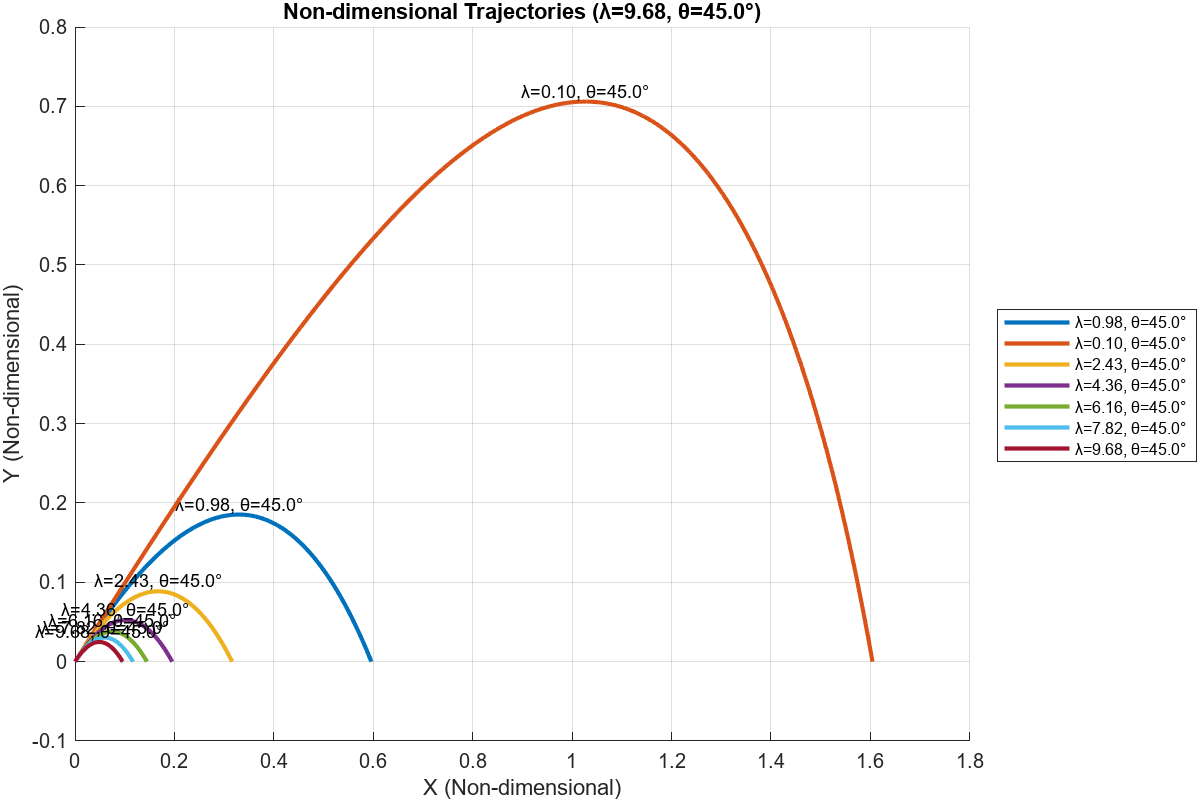
1exportgraphics(app.DimensionalAxes, "dt.png")
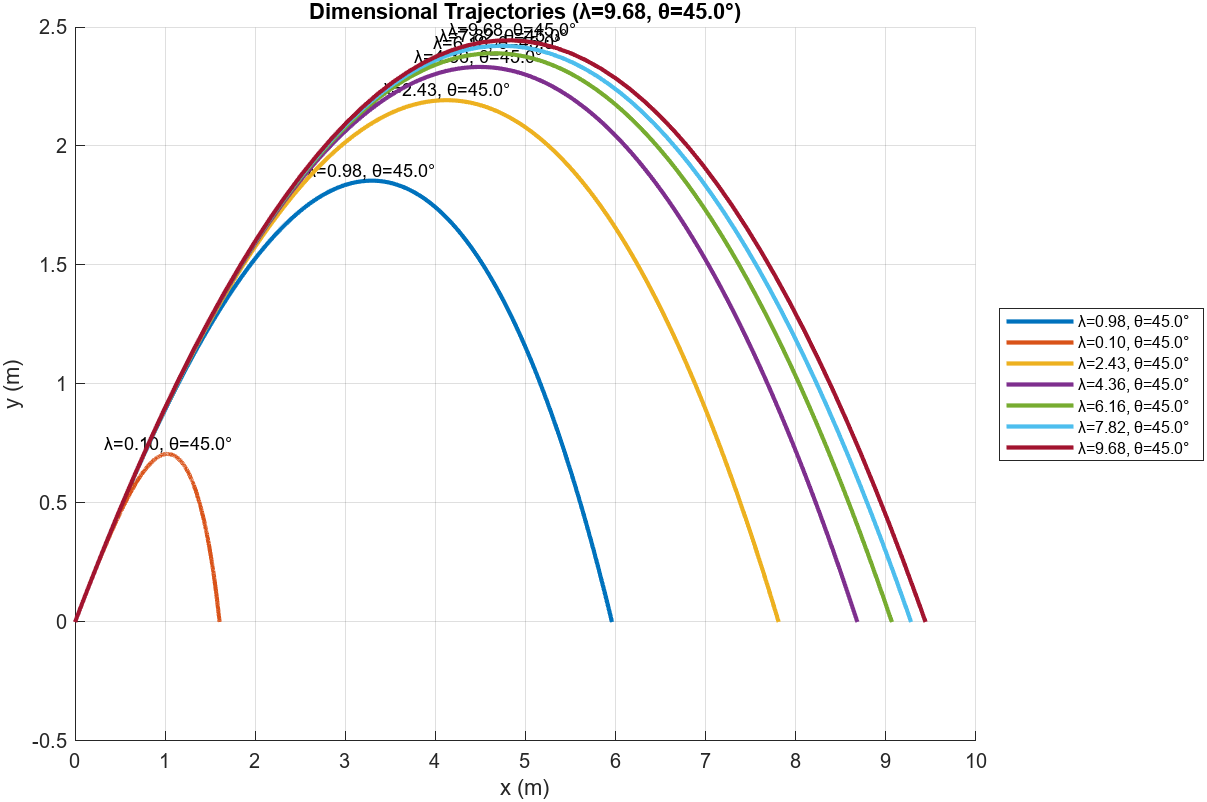
挺好玩的结论:
- 质量越大,有量纲的投射距离越大,但是无量纲的投射距离越小。
- 质量很大之后,有量纲的投射距离会趋于一个定值,但是无量纲的投射距离会趋于0。
因为参考长度为$m/k$,所以质量越大,参考长度越大,这就是上面现象的原因。
至于其他参数的变化,读者可以自行尝试。
完整代码
1classdef ProjectileApp < matlab.apps.AppBase
2 properties
3 % UI Components
4 Figure
5 MainGrid % 主网格布局
6 LeftGrid % 左侧网格布局
7 RightGrid % 右侧网格布局
8 NonDimAxes % 无量纲坐标轴
9 DimensionalAxes % 有量纲坐标轴
10
11 % Tab Group
12 TabGroup
13 TrajectoryTab
14 DimensionalTab
15 SurfaceTab
16
17 % Input Parameters
18 MassEdit
19 DragCoeffEdit
20 GravityEdit
21 VelocityEdit
22 AngleEdit
23
24 % Simulation Parameters
25 Lambda % 无量纲量 mg/(kV^2)
26 LengthScale % 无量纲长度 m/k
27 TimeScale % 无量纲时间 m/(kV)
28 Theta
29
30 % Display Labels
31 LengthScaleLabel
32 TimeScaleLabel
33
34 % Plot Data
35 TimeData
36 XData
37 YData
38
39 % Value Changed Listeners
40 MassListener
41 DragCoeffListener
42 GravityListener
43 VelocityListener
44 AngleListener
45
46 % 最高点显示
47 MaxHeightLabel
48 MaxHeightNondimLabel
49
50 % 3D Plot
51 Surface3DAxes % 三维图坐标轴
52 LambdaRange % lambda 的范围数组
53 ThetaRange % theta 的范围数组
54 RangeData % 存储射程数据的矩阵
55
56 % 轨迹数据存储
57 TrajectoryData % 存储所有轨迹数据的结构体数组
58 TrajectoryLines % 存储所有轨迹线的句柄数组
59 LegendEntries % 存储图例条目
60
61 % 删除按钮
62 ClearButton
63 end
64
65 methods
66 function app = ProjectileApp
67 % 初始化基类
68 app = app@matlab.apps.AppBase();
69
70 % 创建主窗口
71 app.Figure = uifigure('Name', 'Projectile Motion Analysis', ...
72 'Position', [100 100 1200 600]);
73 movegui(app.Figure, 'center');
74
75 % 创建主网格布局 - 2列,左窄右宽
76 app.MainGrid = uigridlayout(app.Figure, [1 2]);
77 app.MainGrid.ColumnWidth = {'3x', '7x'};
78
79 % 创建左侧控制面板网格 - 增加行数以容纳无量纲量显示
80 app.LeftGrid = uigridlayout(app.MainGrid, [11 2]);
81 app.LeftGrid.RowHeight = {'fit', 'fit', 'fit','fit', 'fit', 'fit', 'fit', 'fit', 'fit', 'fit', 'fit'};
82 app.LeftGrid.Padding = [10 10 10 10];
83 app.LeftGrid.RowSpacing = 10;
84
85 % 创建右侧图表网格
86 app.RightGrid = uigridlayout(app.MainGrid, [1 1]);
87 app.RightGrid.Padding = [10 10 10 10];
88
89 % 创建 Tab Group
90 app.TabGroup = uitabgroup(app.RightGrid);
91
92 % 创建轨迹 Tab
93 app.TrajectoryTab = uitab(app.TabGroup);
94 app.TrajectoryTab.Title = 'Non-dimensional';
95
96 % 创建轨迹 Tab 的网格布局
97 trajectoryGrid = uigridlayout(app.TrajectoryTab, [1 1]);
98 trajectoryGrid.Padding = [10 10 10 10];
99
100 % 创建有量纲轨迹 Tab
101 app.DimensionalTab = uitab(app.TabGroup);
102 app.DimensionalTab.Title = 'Dimensional';
103
104 % 创建有量纲轨迹 Tab 的网格布局
105 dimensionalGrid = uigridlayout(app.DimensionalTab, [1 1]);
106 dimensionalGrid.Padding = [10 10 10 10];
107
108 % 创建三维图 Tab
109 app.SurfaceTab = uitab(app.TabGroup);
110 app.SurfaceTab.Title = 'Range Surface';
111
112 % 创建三维图 Tab 的网格布局
113 surfaceGrid = uigridlayout(app.SurfaceTab, [1 1]);
114 surfaceGrid.Padding = [10 10 10 10];
115
116 % 创建输入控件
117 createInputFields(app);
118
119 % 创建轨迹图
120 app.NonDimAxes = uiaxes(trajectoryGrid);
121 app.NonDimAxes.Layout.Row = 1;
122 app.NonDimAxes.Layout.Column = 1;
123 title(app.NonDimAxes, 'Non-dimensional Trajectories');
124 xlabel(app.NonDimAxes, 'X (Non-dimensional)');
125 ylabel(app.NonDimAxes, 'Y (Non-dimensional)');
126 grid(app.NonDimAxes, 'on');
127
128 % 创建有量纲轨迹图
129 app.DimensionalAxes = uiaxes(dimensionalGrid);
130 app.DimensionalAxes.Layout.Row = 1;
131 app.DimensionalAxes.Layout.Column = 1;
132 title(app.DimensionalAxes, 'Dimensional Trajectories');
133 xlabel(app.DimensionalAxes, 'x (m)');
134 ylabel(app.DimensionalAxes, 'y (m)');
135 grid(app.DimensionalAxes, 'on');
136
137 % 创建三维图
138 app.Surface3DAxes = uiaxes(surfaceGrid);
139 app.Surface3DAxes.Layout.Row = 1;
140 app.Surface3DAxes.Layout.Column = 1;
141 title(app.Surface3DAxes, 'Range Surface');
142 xlabel(app.Surface3DAxes, 'λ');
143 ylabel(app.Surface3DAxes, 'θ (deg)');
144 zlabel(app.Surface3DAxes, 'Range (m)');
145 grid(app.Surface3DAxes, 'on');
146 view(app.Surface3DAxes, 45, 30);
147
148 % 初始化三维图
149 calculateRangeSurface(app);
150
151 % 初始化无量纲参数
152 updateDimensionlessParameters(app);
153 end
154
155 function createInputFields(app)
156 % 质量输入
157 lbl = uilabel(app.LeftGrid);
158 lbl.Text = 'Mass (kg):';
159 lbl.Layout.Row = 1;
160 lbl.Layout.Column = 1;
161
162 app.MassEdit = uislider(app.LeftGrid);
163 app.MassEdit.Limits = [0.1 10];
164 app.MassEdit.Value = 1;
165 app.MassEdit.Layout.Row = 1;
166 app.MassEdit.Layout.Column = 2;
167
168 % 阻力系数输入
169 lbl = uilabel(app.LeftGrid);
170 lbl.Text = 'Drag Coefficient (N·s²/m²):';
171 lbl.Layout.Row = 2;
172 lbl.Layout.Column = 1;
173
174 app.DragCoeffEdit = uislider(app.LeftGrid);
175 app.DragCoeffEdit.Limits = [0.01 1];
176 app.DragCoeffEdit.Value = 0.1;
177 app.DragCoeffEdit.Layout.Row = 2;
178 app.DragCoeffEdit.Layout.Column = 2;
179
180 % 重力加速度输入
181 lbl = uilabel(app.LeftGrid);
182 lbl.Text = 'Gravity (m/s²):';
183 lbl.Layout.Row = 3;
184 lbl.Layout.Column = 1;
185
186 app.GravityEdit = uislider(app.LeftGrid);
187 app.GravityEdit.Limits = [1 20];
188 app.GravityEdit.Value = 9.81;
189 app.GravityEdit.Layout.Row = 3;
190 app.GravityEdit.Layout.Column = 2;
191
192 % 初速度输入
193 lbl = uilabel(app.LeftGrid);
194 lbl.Text = 'Initial Velocity (m/s):';
195 lbl.Layout.Row = 4;
196 lbl.Layout.Column = 1;
197
198 app.VelocityEdit = uislider(app.LeftGrid);
199 app.VelocityEdit.Limits = [1 50];
200 app.VelocityEdit.Value = 10;
201 app.VelocityEdit.Layout.Row = 4;
202 app.VelocityEdit.Layout.Column = 2;
203
204 % 角度输入
205 lbl = uilabel(app.LeftGrid);
206 lbl.Text = 'Angle (degrees):';
207 lbl.Layout.Row = 5;
208 lbl.Layout.Column = 1;
209
210 app.AngleEdit = uislider(app.LeftGrid);
211 app.AngleEdit.Limits = [0 90];
212 app.AngleEdit.Value = 45;
213 app.AngleEdit.Layout.Row = 5;
214 app.AngleEdit.Layout.Column = 2;
215
216 % 无量纲量显示
217 lbl = uilabel(app.LeftGrid);
218 lbl.Text = 'Length Scale (m/k):';
219 lbl.Layout.Row = 6;
220 lbl.Layout.Column = 1;
221
222 app.LengthScaleLabel = uilabel(app.LeftGrid);
223 app.LengthScaleLabel.Text = '0';
224 app.LengthScaleLabel.Layout.Row = 6;
225 app.LengthScaleLabel.Layout.Column = 2;
226
227 lbl = uilabel(app.LeftGrid);
228 lbl.Text = 'Time Scale (m/kV):';
229 lbl.Layout.Row = 7;
230 lbl.Layout.Column = 1;
231
232 app.TimeScaleLabel = uilabel(app.LeftGrid);
233 app.TimeScaleLabel.Text = '0';
234 app.TimeScaleLabel.Layout.Row = 7;
235 app.TimeScaleLabel.Layout.Column = 2;
236
237 % 添加最高点显示
238 lbl = uilabel(app.LeftGrid);
239 lbl.Text = 'Max Height (m):';
240 lbl.Layout.Row = 8;
241 lbl.Layout.Column = 1;
242
243 app.MaxHeightLabel = uilabel(app.LeftGrid);
244 app.MaxHeightLabel.Text = '0';
245 app.MaxHeightLabel.Layout.Row = 8;
246 app.MaxHeightLabel.Layout.Column = 2;
247
248 lbl = uilabel(app.LeftGrid);
249 lbl.Text = 'Max Height (Non-dim):';
250 lbl.Layout.Row = 9;
251 lbl.Layout.Column = 1;
252
253 app.MaxHeightNondimLabel = uilabel(app.LeftGrid);
254 app.MaxHeightNondimLabel.Text = '0';
255 app.MaxHeightNondimLabel.Layout.Row = 9;
256 app.MaxHeightNondimLabel.Layout.Column = 2;
257
258 % 创建按钮网格布局
259 buttonGrid = uigridlayout(app.LeftGrid, [2 1]);
260 buttonGrid.Layout.Row = 10;
261 buttonGrid.Layout.Column = [1 2];
262 buttonGrid.RowHeight = {'1x', '1x'};
263 buttonGrid.RowSpacing = 5;
264
265 % 模拟按钮
266 btn = uibutton(buttonGrid);
267 btn.Text = 'Simulate';
268 btn.ButtonPushedFcn = @app.simulateButtonPushed;
269 btn.Layout.Row = 1;
270 btn.Layout.Column = 1;
271
272 % 清空按钮
273 app.ClearButton = uibutton(buttonGrid);
274 app.ClearButton.Text = 'Clear All';
275 app.ClearButton.ButtonPushedFcn = @app.clearButtonPushed;
276 app.ClearButton.Layout.Row = 2;
277 app.ClearButton.Layout.Column = 1;
278
279 % 添加值改变事件监听
280 app.MassListener = listener(app.MassEdit, 'ValueChanged', @(~,~) updateDimensionlessParameters(app));
281 app.DragCoeffListener = listener(app.DragCoeffEdit, 'ValueChanged', @(~,~) updateDimensionlessParameters(app));
282 app.GravityListener = listener(app.GravityEdit, 'ValueChanged', @(~,~) updateDimensionlessParameters(app));
283 app.VelocityListener = listener(app.VelocityEdit, 'ValueChanged', @(~,~) updateDimensionlessParameters(app));
284 app.AngleListener = listener(app.AngleEdit, 'ValueChanged', @(~,~) updateDimensionlessParameters(app));
285 end
286
287 function updateDimensionlessParameters(app)
288 % 获取当前参数
289 m = app.MassEdit.Value;
290 k = app.DragCoeffEdit.Value;
291 g = app.GravityEdit.Value;
292 V = app.VelocityEdit.Value;
293 theta_deg = app.AngleEdit.Value;
294
295 % 计算无量纲参数
296 app.LengthScale = m/k;
297 app.TimeScale = m/(k*V);
298 app.Lambda = m*g/(k*V^2);
299 app.Theta = theta_deg * pi/180;
300
301 % 更新显示
302 app.LengthScaleLabel.Text = sprintf('%.2f m', app.LengthScale);
303 app.TimeScaleLabel.Text = sprintf('%.2f s', app.TimeScale);
304
305 % 检查是否已存在相同无量纲参数的轨迹
306 if ~isempty(app.TrajectoryData)
307 existingParams = [app.TrajectoryData.params];
308 for i = 1:length(existingParams)
309 % 计算已存在轨迹的无量纲参数
310 existingLambda = existingParams(i).m * existingParams(i).g / ...
311 (existingParams(i).k * existingParams(i).V^2);
312 existingTheta = existingParams(i).theta * pi/180;
313
314 % 使用无量纲参数进行比较
315 if abs(existingLambda - app.Lambda) < 1e-6 && ...
316 abs(existingTheta - app.Theta) < 1e-6
317 % 如果找到相同无量纲参数,直接返回
318 return;
319 end
320 end
321 end
322
323 % 求解ODE
324 [app.TimeData, app.XData, app.YData] = solveDimensionlessODE(app);
325
326 % 计算最高点
327 [maxHeight, maxIdx] = max(app.YData);
328 maxHeightDim = maxHeight * app.LengthScale;
329
330 % 更新最高点显示
331 app.MaxHeightLabel.Text = sprintf('%.2f m', maxHeightDim);
332 app.MaxHeightNondimLabel.Text = sprintf('%.2f', maxHeight);
333
334 % 创建新的轨迹线 - 使用无量纲坐标
335 hold(app.NonDimAxes, 'on');
336 newLine = plot(app.NonDimAxes, app.XData, app.YData, 'LineWidth', 2);
337 hold(app.NonDimAxes, 'off');
338
339 % 创建新的轨迹线 - 使用有量纲坐标
340 hold(app.DimensionalAxes, 'on');
341 newDimensionalLine = plot(app.DimensionalAxes, app.XData * app.LengthScale, app.YData * app.LengthScale, 'LineWidth', 2);
342 hold(app.DimensionalAxes, 'off');
343
344 % 存储轨迹数据 - 同时存储有量纲和无量纲坐标
345 newData = struct('x', app.XData * app.LengthScale, 'y', app.YData * app.LengthScale, ...
346 'X', app.XData, 'Y', app.YData, ...
347 'params', struct('m', m, 'k', k, 'g', g, 'V', V, 'theta', theta_deg));
348 app.TrajectoryData = [app.TrajectoryData, newData];
349 app.TrajectoryLines = [app.TrajectoryLines, newLine, newDimensionalLine];
350
351 % 更新图例
352 legendText = sprintf('λ=%.2f, θ=%.1f°', app.Lambda, theta_deg);
353 app.LegendEntries = [app.LegendEntries, {legendText}];
354
355 % 在最高点添加文本标注
356 [maxY, maxIdx] = max(app.YData);
357 text(app.NonDimAxes, app.XData(maxIdx), maxY, legendText, ...
358 'VerticalAlignment', 'bottom', ...
359 'HorizontalAlignment', 'center');
360
361 % 在有量纲图中添加最高点标注
362 text(app.DimensionalAxes, app.XData(maxIdx) * app.LengthScale, maxY * app.LengthScale, legendText, ...
363 'VerticalAlignment', 'bottom', ...
364 'HorizontalAlignment', 'center');
365
366 % 将图例移到坐标轴外部
367 legend(app.NonDimAxes, app.LegendEntries, 'Location', 'eastoutside');
368 legend(app.DimensionalAxes, app.LegendEntries, 'Location', 'eastoutside');
369
370 % 设置坐标轴范围为自动
371 axis(app.NonDimAxes, 'auto');
372 axis(app.DimensionalAxes, 'auto');
373
374 % 更新标题
375 title(app.NonDimAxes, sprintf('Non-dimensional Trajectories (λ=%.2f, θ=%.1f°)', app.Lambda, theta_deg));
376 title(app.DimensionalAxes, sprintf('Dimensional Trajectories (λ=%.2f, θ=%.1f°)', app.Lambda, theta_deg));
377
378 % 更新三维图
379 calculateRangeSurface(app);
380 end
381
382 function simulateButtonPushed(app, ~, ~)
383 % 直接调用updateDimensionlessParameters来更新轨迹
384 updateDimensionlessParameters(app);
385 end
386
387 function [T, X, Y] = solveDimensionlessODE(app)
388 % 初始条件
389 X0 = 0;
390 Y0 = 0;
391 Xp0 = cos(app.Theta);
392 Yp0 = sin(app.Theta);
393
394 % 求解ODE直到Y回到初始高度
395 y0 = [X0; Y0; Xp0; Yp0];
396 options = odeset('Events', @(t,y) heightEvent(t,y,Y0), ...
397 'RelTol', 1e-8, ... % 相对误差
398 'AbsTol', 1e-8, ... % 绝对误差
399 'MaxStep', 0.01); % 最大步长
400 [T, Y] = ode45(@(t,y) dimensionlessODE(t, y, app.Lambda), [0 100], y0, options);
401
402 X = Y(:,1);
403 Y = Y(:,2);
404 end
405
406 function calculateRangeSurface(app)
407 % 创建lambda和theta的网格
408 app.LambdaRange = linspace(0.01, 100, 20);
409 app.ThetaRange = linspace(1, 90, 20); % 从1度开始,而不是0度
410 [Lambda, Theta] = meshgrid(app.LambdaRange, app.ThetaRange);
411 app.RangeData = zeros(size(Lambda));
412
413 % 计算每个点的最终x距离
414 for i = 1:length(app.ThetaRange)
415 for j = 1:length(app.LambdaRange)
416 lambda = Lambda(i,j);
417 theta = Theta(i,j) * pi/180;
418
419 % 求解ODE直到Y回到初始高度
420 y0 = [0; 0; cos(theta); sin(theta)];
421 options = odeset('Events', @(t,y) heightEvent(t,y,0), ...
422 'RelTol', 1e-8, ...
423 'AbsTol', 1e-8, ...
424 'MaxStep', 0.01);
425 [~, Y] = ode45(@(t,y) dimensionlessODE(t, y, lambda), [0 100], y0, options);
426
427 % 检查是否有解
428 if ~isempty(Y)
429
430 % 获取最终x距离(转换为有量纲)
431 % Y(end,1)是物体落地时的x坐标,Y(end,2)是y坐标(应该接近0)
432 if abs(Y(end,2)) < 1e-6 % 确保物体确实落地
433 app.RangeData(i,j) = Y(end,1) * lambda;
434 else
435 % 如果物体没有正确落地,设置为NaN
436 app.RangeData(i,j) = NaN;
437 end
438 else
439 % 如果没有解,设置为NaN
440 app.RangeData(i,j) = NaN;
441 end
442 end
443 end
444
445 % 绘制三维图
446 surf(app.Surface3DAxes, Lambda, Theta, app.RangeData);
447 colorbar(app.Surface3DAxes);
448 shading(app.Surface3DAxes, 'interp');
449
450 % 更新标签
451 title(app.Surface3DAxes, 'Range Surface');
452 xlabel(app.Surface3DAxes, 'λ');
453 ylabel(app.Surface3DAxes, 'θ (deg)');
454 zlabel(app.Surface3DAxes, 'Range (m)');
455
456 % 在当前参数位置添加标记
457 % hold(app.Surface3DAxes, 'on');
458 % plot3(app.Surface3DAxes, app.Lambda, app.Theta*180/pi, ...
459 % app.XData(end) * app.LengthScale, 'ro', 'MarkerSize', 10, 'MarkerFaceColor', 'r');
460 % hold(app.Surface3DAxes, 'off');
461 end
462
463 function clearButtonPushed(app, ~, ~)
464 % 清除所有轨迹线
465 if ~isempty(app.TrajectoryLines)
466 delete(app.TrajectoryLines);
467 app.TrajectoryLines = [];
468 end
469
470 % 清除所有轨迹数据
471 app.TrajectoryData = [];
472
473 % 清除图例
474 app.LegendEntries = {};
475 legend(app.NonDimAxes, 'off');
476 legend(app.DimensionalAxes, 'off');
477
478 % 清除坐标轴上的文本标注
479 for ax = [app.NonDimAxes, app.DimensionalAxes]
480 children = get(ax, 'Children');
481 for i = 1:length(children)
482 if isa(children(i), 'matlab.graphics.primitive.Text')
483 delete(children(i));
484 end
485 end
486 end
487
488 % 重置坐标轴
489 axis(app.NonDimAxes, 'auto');
490 axis(app.DimensionalAxes, 'auto');
491
492 % 更新标题
493 title(app.NonDimAxes, 'Non-dimensional Trajectories');
494 xlabel(app.NonDimAxes, 'X (Non-dimensional)');
495 ylabel(app.NonDimAxes, 'Y (Non-dimensional)');
496
497 title(app.DimensionalAxes, 'Dimensional Trajectories');
498 xlabel(app.DimensionalAxes, 'x (m)');
499 ylabel(app.DimensionalAxes, 'y (m)');
500
501 % 更新三维图
502 calculateRangeSurface(app);
503 end
504 end
505end
506
507function [value, isterminal, direction] = heightEvent(t, y, Y0)
508% 当Y回到初始高度时停止
509value = y(2) - Y0; % 当前高度与初始高度的差
510isterminal = 1; % 停止积分
511direction = -1; % 只在下降穿过初始高度时停止
512end
513
514function dydt = dimensionlessODE(t, y, lambda)
515% y = [X; Y; X'; Y']
516X = y(1);
517Y = y(2);
518Xp = y(3);
519Yp = y(4);
520
521% Calculate velocity magnitude
522V = sqrt(Xp^2 + Yp^2);
523
524% ODE system
525dydt = zeros(4,1);
526dydt(1) = Xp;
527dydt(2) = Yp;
528dydt(3) = -V * Xp;
529dydt(4) = -V * Yp - lambda;
530end
总结
量纲分析,通过量纲组合,把一个依赖于多个物理量的函数,简化为一个依赖于较少的无量纲量的函数,这非常有助于我们对问题的理解,并且可以指导我们进行实验设计。
文章标签
|-->dimensional analysis |-->dynamics |-->matlab |-->ode45 |-->ode |-->uifigure |-->App Designer
- 本站总访问量:loading次
- 本站总访客数:loading人
- 可通过邮件联系作者:Email大福
- 也可以访问技术博客:大福是小强
- 也可以在知乎搞抽象:知乎-大福
- Comments, requests, and/or opinions go to: Github Repository
