2025-03-29 |欢迎您，第位读者！|

Complexity算法复杂度的基本概念

算法复杂度

CATAM 课程笔记-算法复杂度¹是一个写得很简单、很清晰的关于算法复杂度的课程笔记。

算法复杂度的目的是评估和选择不同的算法来完成同一个计算任务，最基础的目的就是比较不同算法所需要的时间。如果更加严格一些，应该是比较不同算法所需要的资源，时间就是其中的一种最为重要的资源，其他诸如空间、内存、硬盘、网络带宽等都是可以量化的资源。我们在评价算法时，通常会考虑这个算法所解决问题的规模，因为不同规模的相同问题，对所需要的资源可能会有差异。而且，规模，通常会是算法开发和算法实际应用时需要考虑的最重要因素之一。

比如我们讨论微分方程的积分，那么积分的步数，可能就是一个恰当的规模指标；当我们讨论矩阵乘法时，矩阵的阶数，可能就是一个恰当的规模指标。

另外，我们通常会采用一个很模糊的概念来作为指标评价算法，就是需要操作的次数（步数），而不是实际运行的时间。这主要是因为，实际运行时间会受到很多因素的影响，比如计算机硬件的性能、运行时环境等。而用一个稍微抽象一点的指标来评价算法，则可以更加客观地比较不同算法。例如，我们在评价一个需要调用一定次数加法和乘法的算法时，我们通常会选择乘法的次数（步数）作为衡量指标，因为在大多数计算架构中，乘法比加法更加耗时。但是，如果我们能实现一个乘法机（乘法芯片），而把加法实现为乘法的组合，那么选择加法的次数作为衡量指标，可能更加合适。

总结来看，算法复杂度的评价，需要考虑如下的映射。

其中，$N$ 是问题的规模，$C(N)$ 是算法在解决这个问题时所需要的操作次数。

例一

计算这个和，需要$2n$次乘法和$n-1$次加法。通常我们会把这个计算的复杂度即为$\mathcal{O}(n)$。也就是时间大概和$n$成正比，当然实际上，$n$越大，这个比例关系越精确。因为单次乘法的时间还会受到随机因素的影响，当$n$够大时，这个影响就会被平均掉。

如果我们用公式来计算上面的和

计算这个和，需要$4$次乘法和$2$次加法。通常我们会把这个计算的复杂度即为$\mathcal{O}(1)$。

通过这个例子，我们可以看到$\mathcal{O}(\cdot)$的计数法中：

• 加起来的常数项，可以忽略不计，取为0
• 只计算最高次项，忽略低次项
• 乘法中的常数，可以忽略，取为1

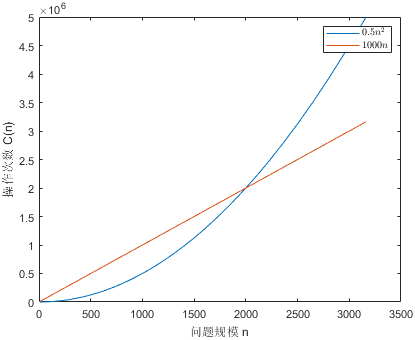
因为这个原因，只有在$n$足够大时，上面的 $\mathcal{O}(\cdot)$ 的计数法才有意义。为了说明这一点，我们比较一个$n$和$n^2$的计算复杂度。比如一个算法的操作次数为$0.5 * n^2$，另外一个算法的操作次数为$1000 * n$。

1n = logspace(1, 3.5, 100);
2plot(n, 0.5 * n.^2, n, 1000 * n);
3legend({'$0.5 n^2$', '$1000 n$'}, Interpreter='latex')
4xlabel('问题规模 n')
5ylabel('操作次数 C(n)')
6exportgraphics(gcf, 'complexity.png', 'Resolution', 80)

从图中可以看到，只有当$n \ge 2000$时，$0.5 n^2$的算法才比$1000 n$的算法步数更多。所以，还可以再强调一遍，只有当$n \to \infty$时，$\mathcal{O}(\cdot)$才能反映出算法的复杂度。

例二

考虑两个矩阵的乘法，第一个矩阵大小为$n \times m$，第二个矩阵大小为$m \times p$，那么乘法运算的次数为$n \times m \times p$，我们可以忽略加法的次数，把这个复杂度记为$\mathcal{O}(nmp)$。当两个相乘的矩阵中，$n=m=p$时，复杂度为$\mathcal{O}(n^3)$。

当然，还存在一个更高效的算法，就是Strassen算法²，它把复杂度降低到了$\mathcal{O}(n^{\log_2 7})$。

例三

考虑排序一个列表，可能是数字，也可能是字符串，这在处理实际的数据和信息时，是非常常见的操作。比较不同排序算法的基本操作是比较。最有效的排序算法可以只需要$\mathcal{O}(n \log n)$次比较。非常简单的冒泡排序需要$\mathcal{O}(n^2)$次比较。

进一步的讨论

通常而言，一个算法总是会有一些额外开销，例如前面所说的，忽略的加法消耗（计算步数时忽略的部分）、或者在计算步数时去掉的低阶部分（例如$4 + 5n + \frac{1}{3} n^3$会被写为$\mathcal{O}(n^3)$）、或者在计算式耗费的固定部分。例如，要计算

首先就需要计算三次方根，然后取整，然后计算阶乘。那么这里的开方和取整，就是固定开销，而阶乘就是变量开销，这个整个复杂度就写成

另外，还有两个跟复杂度 $\mathcal{O}(\cdot)$ 相关的概念。一个记为$\Omega(\cdot)$，一个记为$\Theta(\cdot)$。在这个含义下，近似的说法应该是：

• $\mathcal{O}(\cdot)$ 表示当$n$足够大时，算法的复杂度不会超过$\mathcal{O}(\cdot)$
• $\Omega(\cdot)$ 表示当$n$足够大时，算法的复杂度不会低于$\Omega(\cdot)$
• $\Theta(\cdot)$ 表示当$n$足够大时，算法的复杂度既不会超过$\Theta(\cdot)$，也不会低于 $\Theta(\cdot)$，也就是相当于是 $\mathcal{O}(\cdot)$ 和 $\Omega(\cdot)$的交集

大概，算法复杂度，最基本的只需了解这些概念，就足够了。