Compare_Matrix_Squre_Sum_in_MATLAB中矩阵平方和的比较
矩阵平方和的计算
矩阵平方和的定义
矩阵平方和的定义是对矩阵中的每一个元素进行平方,然后求和。
对于一个矩阵$A$,其平方和定义为:
$$ \text{sum} = \sum_{i=1}^{m}\sum_{j=1}^{n} A(i,j)^2 $$这个平方和计算,在某些机器学习的算法中、或者特殊的优化问题中都会涉及到。
矩阵平方和的计算方法
通常而言,前面的公式就给出了计算的方法,无论怎么做,都会涉及到对矩阵中的每一个元素进行平方,然后求和。 因此算法的时间复杂度是$O(m*n)$,其中$m$是矩阵的行数,$n$是矩阵的列数,当$A$是方阵时,$m=n$。 最终,算法的效率取决于矩阵的表示形式和对矩阵元素的访问方式。 当然,还有可能会有一些特殊的优化方法,比如矩阵的特殊性质,可以通过一些特殊的方法来计算,这里不做考虑。
最后,就是并行指令集的使用,比如SIMD指令集,这里也不进行相关的讨论。
下面,就主要是对在Matlab中实现矩阵平方和的几种方法进行比较。其实比较的是Matlab中访问矩阵元素的方式的性能差异。
Matlab的若干实现
我们非常随意的实现了一些方法。
其中最重要的就是所谓的基线方法。这个方法通常选择一个最简单/直观的方法,便于抓住算法中的核心要素。 然后作为对比的基准,也能够对不同算法的性能进行比较。
这种研究办法,是一种常见的研究方法。例如,在优化算法中,通常选择格子搜索或者随机搜索作为基线方法。 提出一种新的方法,通常希望能够对比基线方法有更好的性能,并且这种性能提升是显著的。 此外,也会结合新算法与基线算法的执行过程来解释算法优势的原理,这就是一般算法研究文章中非常重要的理论分析。
1function sumRet = bench_loop_row_column(A)
2 % 按照行、列的方式进行循环求和,基线算法
3 % 内存:O(1)
4 % 时间:O(m*n) ~ O(n^2)
5 [m, n] = size(A);
6 sumRet = 0;
7 % 对行进行循环
8 for i = 1:m
9 % 对列进行循环
10 for j = 1:n
11 sumRet = sumRet + A(i, j) ^ 2;
12 end
13
14 % 列循环结束
15 end
16
17 % 行循环结束,
18end
上面这个最为直观的算法,就是对矩阵的每一行进行遍历,然后对每一行的每一个元素进行平方,然后求和。 这个作为基线是一个恰当的选择。
相应的,我们就会想到先循环列,再循环行来作为对基线算法的改进。
1function sumRet = bench_loop_column_row(A)
2 % 按照列、行的方式进行循环求和,第一次改进的算法
3 % 充分考虑到矩阵的存储方式:列优先
4 % 内存:O(1)
5 % 时间:O(m*n) ~ O(n^2)
6 [m, n] = size(A);
7 sumRet = 0;
8
9 for i = 1:n
10
11 for j = 1:m
12 sumRet = sumRet + A(j, i) ^ 2;
13 end
14
15 end
16
17end
考虑到Matlab能够直接索引列,我们就可以考虑对每列进行循环,直接对列进行操作。或者,换成对行进行操作。
下面几个算法就是行、列操作的形式,这里又有一个小小的差别,就是使用更多内存来直接进行向量加法,最后调用sum求和。
或者还可以在循环内部调用sum函数,这样内存的使用会从$\mathcal{O}(n)$降低到
1function s = bench_loop_column_sum(A)
2 % 直接循环列,采用向量化的方式访问每个列
3 % 用一个向量来存储每一列和
4 % 最终调用sum函数求和
5 % 内存:O(n)
6 % 时间:考虑到,向量加法的时间复杂度是O(n)
7 % 所以,这里的时间复杂度依然是O(m*n) ~ O(n^2)
8 N = size(A, 2);
9 v = zeros(size(A, 1), 1);
10
11 for i = 1:N
12 v = v + A(:, i) .^ 2;
13 end
14
15 s = sum(v);
16end
1function s = bench_loop_sum_column(A)
2 % 直接循环列,采用向量化的方式访问每个列
3 % 直接对列调用sum函数求列和,最终累加求和
4 % 内存:O(1)
5 % 时间:O(m*n) ~ O(n^2),这里同样认为.^ 的时间复杂度是O(n)
6 s = 0;
7 N = size(A, 2);
8
9 for i = 1:N
10 s = s + sum(A(:, i) .^ 2);
11 end
12
13end
1function s = bench_loop_row_sum(A)
2 % 直接循环行,采用向量化的方式访问每行
3 % 用一个向量来存储行和
4 % 最终调用sum函数求和
5 % 内存:O(n)
6 % 时间:考虑到,向量加法的时间复杂度是O(n)
7 % 所以,这里的时间复杂度依然是O(m*n) ~ O(n^2)
8 N = size(A, 1);
9 v = zeros(1, size(A, 2));
10
11 for i = 1:N
12 v = v + A(i, :) .^ 2;
13 end
14
15 s = sum(v);
16end
1function s = bench_loop_sum_row(A)
2 % 直接循环行,采用向量化的方式访问每个行
3 % 直接对行调用sum函数求行和,最终累加求和
4 % 内存:O(1)
5 % 时间:O(m*n) ~ O(n^2),这里同样认为.^ 的时间复杂度是O(n)
6 s = 0;
7 N = size(A, 1);
8
9 for i = 1:N
10 s = s + sum(A(i, :) .^ 2);
11 end
12
13end
接下来,我们利用矩阵的向量访问方式来构造一个算法。
1function s = bench_loop_vec(A)
2 % 直接将矩阵展开成一个向量,循环求和
3 % 内存:O(1)
4 % 时间:O(m*n) ~ O(n^2)
5 s = 0;
6 N = numel(A);
7
8 for i = 1:N
9 s = s + A(i) .^ 2;
10 end
11
12end
此外,sum函数也提供了两个算法变体,一个是调用两次(默认对行求和)
1function s = bench_sum_sum(A)
2 % 直接两次调用sum函数,对矩阵进行求和
3 s = sum(sum(A .^ 2));
4end
1function s = bench_sum_all(A)
2 % 直接调用一次sum函数,对矩阵进行求和
3 s = sum(A .^ 2, 'all');
4end
还可以把sum与矩阵列向量访问形式结合起来,构成一种算法。
1function s = bench_sum_vec(A)
2 % 直接将矩阵展开成一个向量
3 % 进行元素.^计算,调用sum函数求和
4 s = sum(A(:) .^ 2);
5end
最后还是利用矩阵的向量展开方式,就是两个其实一样的算法,因为dot函数内部就是调用矩阵乘法。
1function s = bench_vec_dot(A)
2 % 直接将矩阵展开成一个向量,进行点积计算
3 s = dot(A(:), A(:));
4end
1function s = bench_matrix_mul(A)
2 % 直接将矩阵展开成一个向量,进行矩阵乘法计算
3 s = A(:).' * A(:);
4end
这些算法都非常平常,但是,通过上面的联系,也能提升我们对Matlab的矩阵操作的理解。 接下来就是对这些算法的性能进行比较。
性能比较
性能比较方法
时间性能比较,一般可以直接利用timeit函数来完成,这个函数会对一个函数进行多次调用,然后求中位数。
这个函数还能包括输出变量的构造时间。
利用这个函数,我们编了一个工具,对不同规模的矩阵进行比较。 这里代码的注释非常清楚,无需赘述。
1%% Benchmark functions helper
2function [n, result] = bench_f_n(n, f)
3 % 按照给定的参数,对函数进行测试
4 % n: 矩阵大小
5 % f: 函数句柄
6 % 返回值:n, result
7 % n: 矩阵大小的向量, result: 运行时间的向量
8 arguments
9 n (:, :) {mustBePositive}
10 f function_handle
11 end
12
13 % 保证n是一个向量,并且是正整数
14 n = round(n(:));
15 result = zeros(1, numel(n));
16 % 对每一个n进行测试,直接采用for循环,不使用arrayfun
17 for i = 1:numel(n)
18 A = rand(n(i), n(i));
19 result(i) = timeit(@()f(A));
20 end
21
22 % result = arrayfun(@(x) timeit(@()f(rand(x, x))), n);
23 % 这样也是可以的,但是,对于此处,上面的写法更加直观
24 % 这就是采用for循环的地方
25 % 为了代码的可读性,并且对性能的影响不大,因为这里的循环次数不多
26end
性能比较代码
我们把前面的算法代码和上面的性能比较代码放在一个+benchobjs的目录中,就构成一个namespace命名空间,通过import benchobjs.*来导入这些函数。
编写如下的测试脚本:
- Matlab code
- 设置测试范围
- 运行测试获取数据
- 可视化测试结果
1%% import functions in benchobjs
2import benchobjs.*;
3
4%% setup problem
5n = round(logspace(3, 4, 10));
6functions = {@bench_loop_row_column, @bench_loop_column_row, ...
7 @bench_loop_column_sum, @bench_loop_sum_column, ...
8 @bench_loop_row_sum, @bench_loop_sum_row, ...
9 @bench_loop_vec, @bench_sum_sum, ...
10 @bench_sum_all, @bench_sum_vec, ...
11 @bench_vec_dot, @bench_matrix_mul};
12markers = {'o', 'x', '+', '*', 's', 'd', '^', 'v', '>', '<', 'p', 'h'};
13% 这里是常见的小技巧,将函数的句柄存储在一个cell数组中
14% 这样可以方便的对这些函数进行遍历
15% 同时,把线型标签也存储在一个cell数组中,这样可以方便的对这些线型进行遍历
16
17%% calculation
18results = cell(numel(functions), 2);
19
20for i = 1:numel(functions)
21 [n, result] = bench_f_n(n, functions{i});
22 results{i, 1} = n;
23 results{i, 2} = result;
24 fprintf('%s: %s: %s\n', func2str(functions{i}), ...
25 mat2str(n), mat2str(result));
26end
27
28cmd = sprintf('save compareMatrixSquareSum%d results', maxNumCompThreads);
29eval(cmd);
30
31% 这里试图考虑到多线程的影响,目前在12核心的及其上进行了不同线程数的测试
32% 发现对于这个问题,多线程并没有展现出过大的差别
33%% Visualize
34% 一般也会把原始数据画出来稍微看一下
35% 为了确保数据的正确性,并且可以对数据进行初步的分析
36figure;
37clf;
38
39for i = 1:numel(functions)
40 [n, result] = results{i, :};
41 plot(n, result, 'LineWidth', 2, 'Marker', markers{i});
42 yscale('log');
43 hold on;
44 fprintf('%s: %s: %s\n', func2str(functions{i}), ...
45 mat2str(n), mat2str(result));
46end
47
48legend(cellfun(@(f)cellref(split(func2str(f), '.'), 2), ...
49 functions, 'UniformOutput', false), ...
50 'Location', 'BestOutSide', "interpreter", "none");
51xlabel('Matrix size');
52ylabel('Time (s)');
53grid on
54
55% exportgraphics(gcf, '../matlab-img/compareMatrixSquareSum-time.png', ...
56% 'Resolution', 600);
57
58%% Visualize 2
59% 针对基准的加速比,这是最常见的基准测试结果的展示方式
60figure;
61clf;
62
63for i = 2:numel(functions)
64 [n, result] = results{i, :};
65 plot(n, results{1, 2} ./ result, ...
66 'LineWidth', 2, 'Marker', markers{i});
67 hold on;
68 fprintf('%s: %s: %s\n', func2str(functions{i}), ...
69 mat2str(n), mat2str(result));
70end
71
72legend(cellfun(@(f)cellref(split(func2str(f), '.'), 2), ...
73 functions(2:numel(functions)), 'UniformOutput', false), ...
74 'Location', 'BestOutSide', "interpreter", "none");
75xlabel('Matrix size');
76ylabel('Time (s)');
77grid on
78
79% exportgraphics(gcf, '../matlab-img/compareMatrixSquareSum-acc.png', ...
80% 'Resolution', 600);
81
82%% Visualize 2
83% 去掉基准和两个最好的函数,这样可以进行更加细节的比较和分析
84% 这里必要性不太大,主要是为了展示这种方式
85figure;
86clf;
87
88for i = 2:numel(functions) - 2
89 [n, result] = results{i, :};
90 plot(n, results{1, 2} ./ result, ...
91 'LineWidth', 2, 'Marker', markers{i});
92 hold on;
93 fprintf('%s: %s: %s\n', func2str(functions{i}), ...
94 mat2str(n), mat2str(result));
95end
96
97legend(cellfun(@(f)cellref(split(func2str(f), '.'), 2), ...
98 functions(2:numel(functions) - 2), 'UniformOutput', false), ...
99 'Location', 'BestOutSide', "interpreter", "none");
100xlabel('Matrix size');
101ylabel('Time (s)');
102grid on
103
104% exportgraphics(gcf, '../matlab-img/compareMatrixSquareSum-acc-2.png',...
105% 'Resolution', 600);
性能比较结果
最终,可以得到如下的性能比较结果。
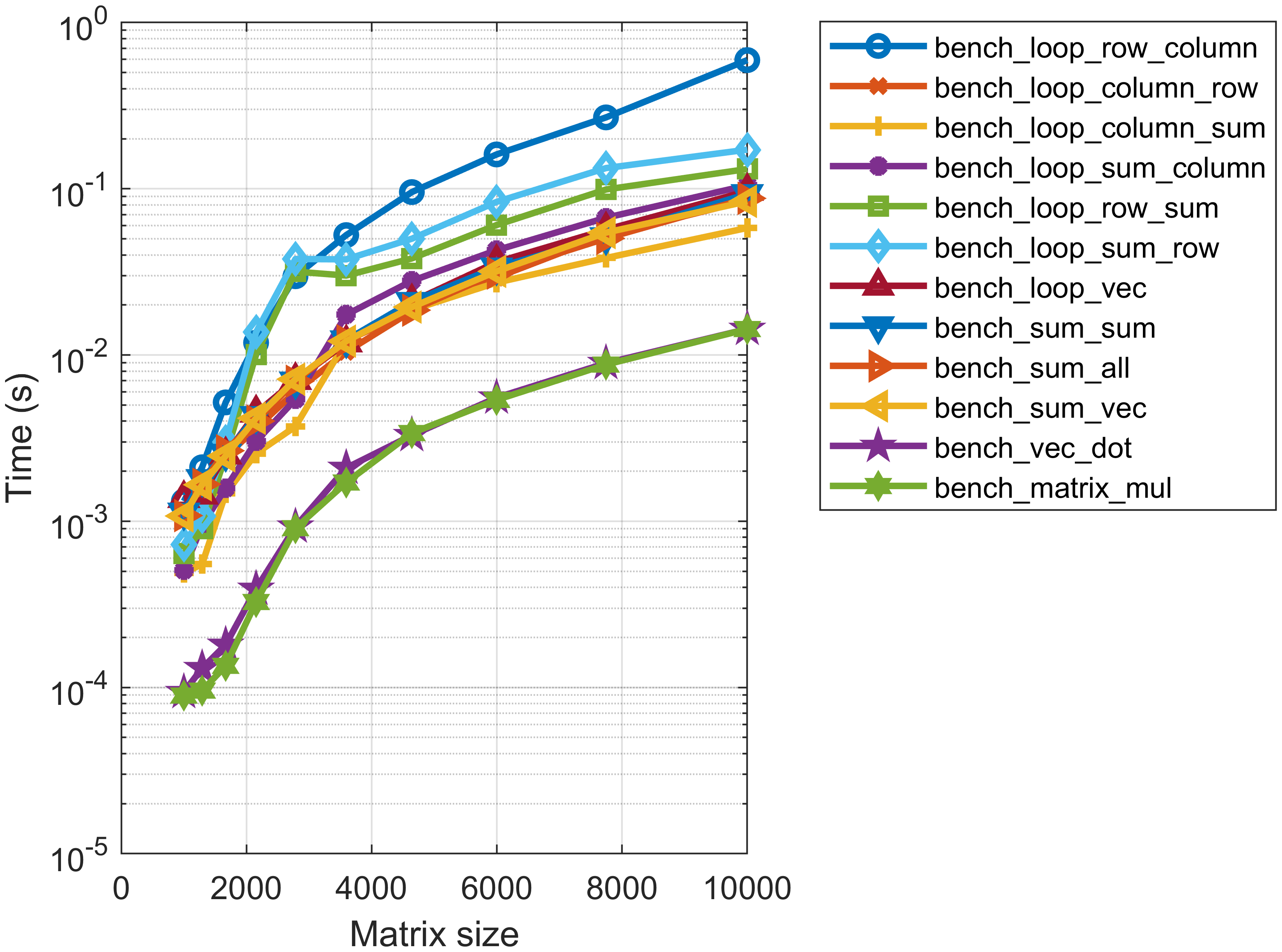
首先,不同算法的性能有一定差异。基本上,算法分为两组,也可以视为三组。
- 第一组是基线算法,对每一行进行遍历,然后对每一个元素进行平方,然后求和。
- 第二组是向量展开访问并调用矩阵乘法(
mtimes直接调用BLAS二进制库)的两个算法,性能相当。 - 其他就是各种循环的组合以及
sum函数的组合。
这个分组,按照加速比来看,更加明显。 向量展开+矩阵乘法的算法在1000~10000的规模下,性能均有显著提升,从15倍到40倍。
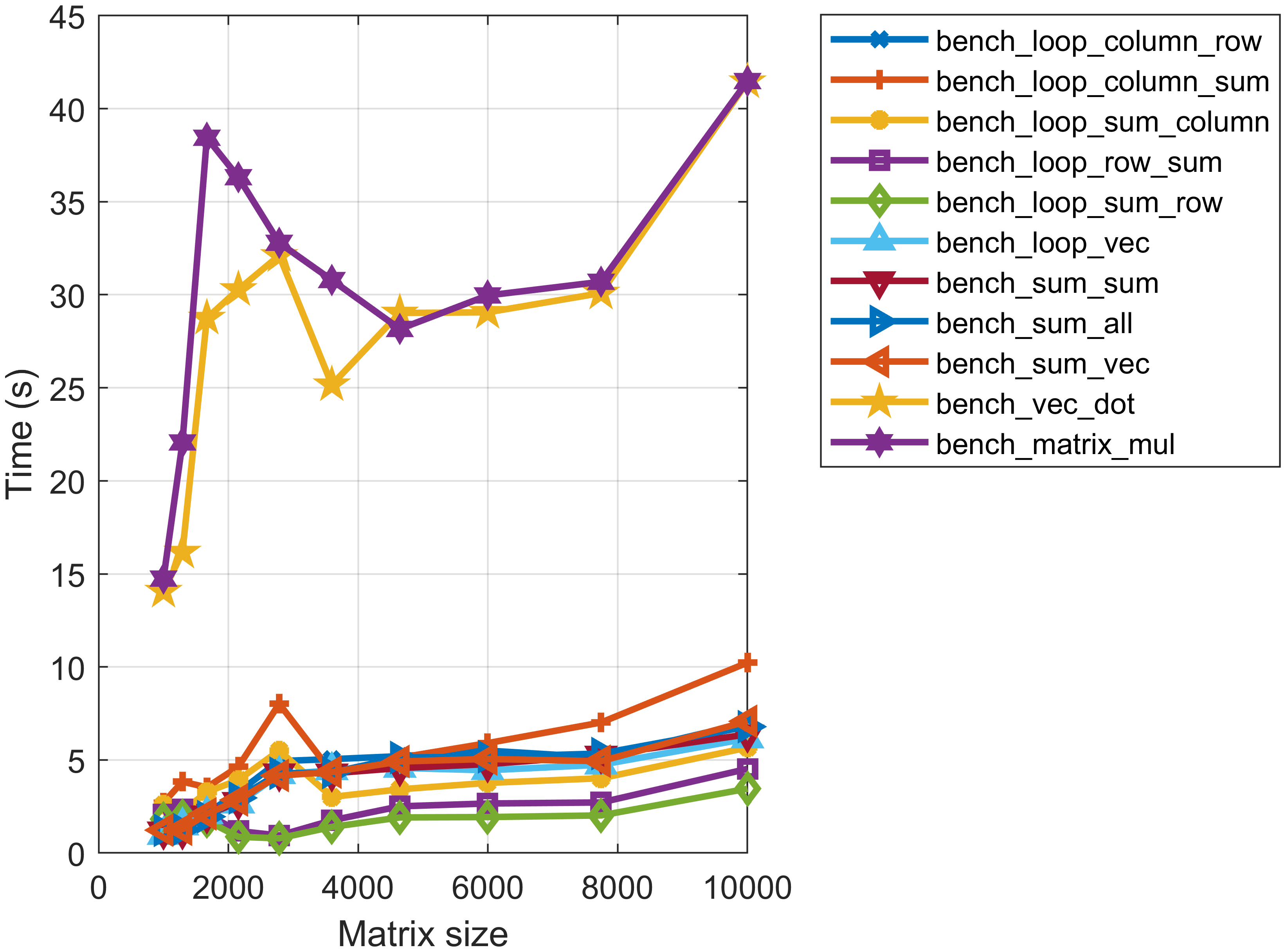
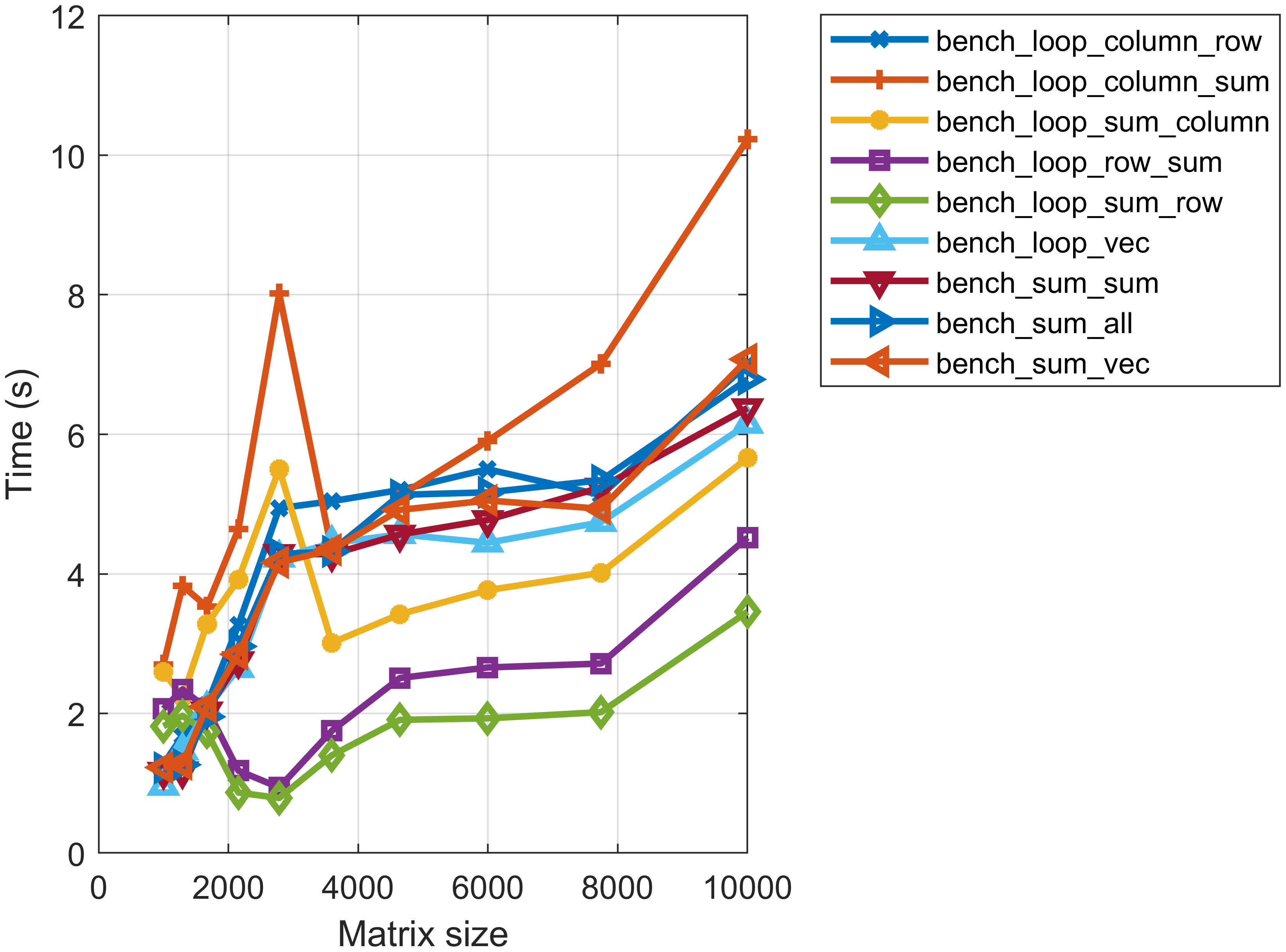
除去基线算法和向量化算法,其他算法的关系较为复杂,但是也能通过进行列访问、部分向量化来获得几倍的性能提升。 这充分显示了列优先矩阵访问对与计算效率的影响。
总结
- 进行算法开发,一定要按照基线算法、算法优化的思路来考虑。
- 对算法的效率进行比较,最好选择不同的规模来分析问题。
- 加速比是一个很好的指标,能够直观的看出算法的性能提升。
文章标签
|-->matlab |-->performance |-->matrix |-->tutorial |-->benchmark |-->algorithm
- 本站总访问量:loading次
- 本站总访客数:loading人
- 可通过邮件联系作者:Email大福
- 也可以访问技术博客:大福是小强
- 也可以在知乎搞抽象:知乎-大福
- Comments, requests, and/or opinions go to: Github Repository
