分解的阶次选择 #
基本概念 #
对于POD和DMD都涉及到$\tau$的选择问题。 这个参数确定了分解后的模态数量和重构的精度。 当然,分解的模态还可以用于分析流动的物理特性,请参考DMD的物理意义中对$D = ABC$的介绍。
POD的阶次选择 #
对于POD而言,阶次的选择相对直观。 因为SVD分解的奇异值是单调递减的, $\sigma_i$ 表示第$i$个特征值, 随着$i$的增大,$\sigma_i$ 逐渐减小。
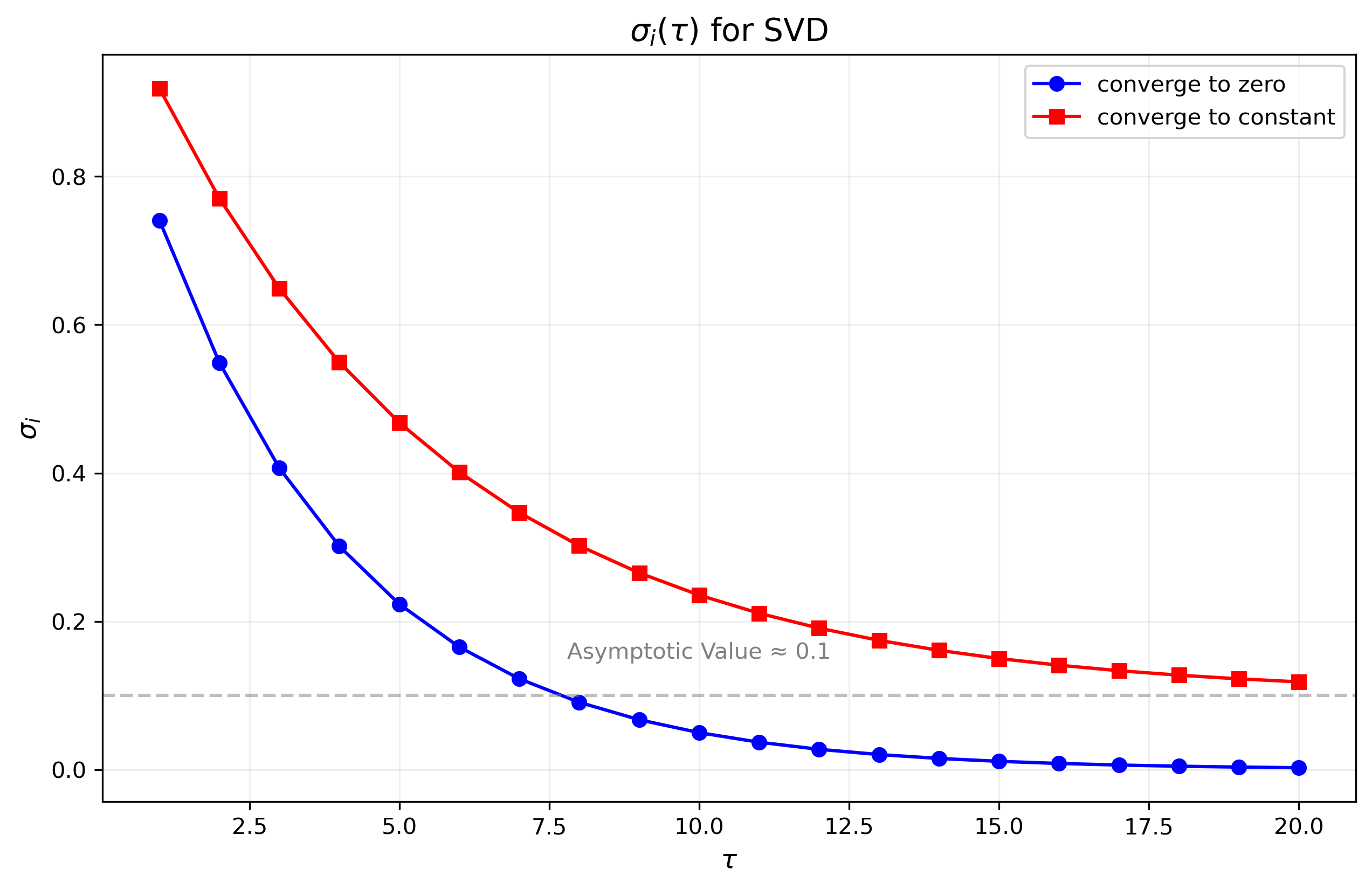
基本上有两个方法来确定$\tau$,一个根据$\sigma_i$的大小,一个根据$\sigma_i$的斜率(变化率)。
- 确定一个阈值,当奇异值小于该阈值时,认为该模态对流场的贡献可以忽略不计。
- 根据增大$\tau$时,$\sigma_i(\tau)$的值不再显著变化,认为此时$\tau$已经取到合适的值。
DMD的阶次选择 #
对于DMD而言,阶次的选择相对复杂。
在DMD方法中,借此的出现是对$\mathbf{X}_1$进行SVD分解, 此时可以选择$\tau$个奇异值最大的模态。 接下来,就需要计算复数矩阵$S$的特征值构成的向量$\mu$。每一个$\mu_i$对应于复平面上的点:
- 当这个点位于单位圆上时,对应的模态是稳定的
- 当这个点位于单位圆内时,对应的模态是衰减的,当该店接近圆心时对应于噪声
- 当这个点位于单位圆外时,对应的模态是发散的
但是考虑到增益$\mathbf{b}$并没有排序,这里的选择就变得复杂了。如果我们把$b_i$和$\mu_i$画在3D空间中, 就能得到完整的时间域的系统行为(综合了时间模态和增益)。
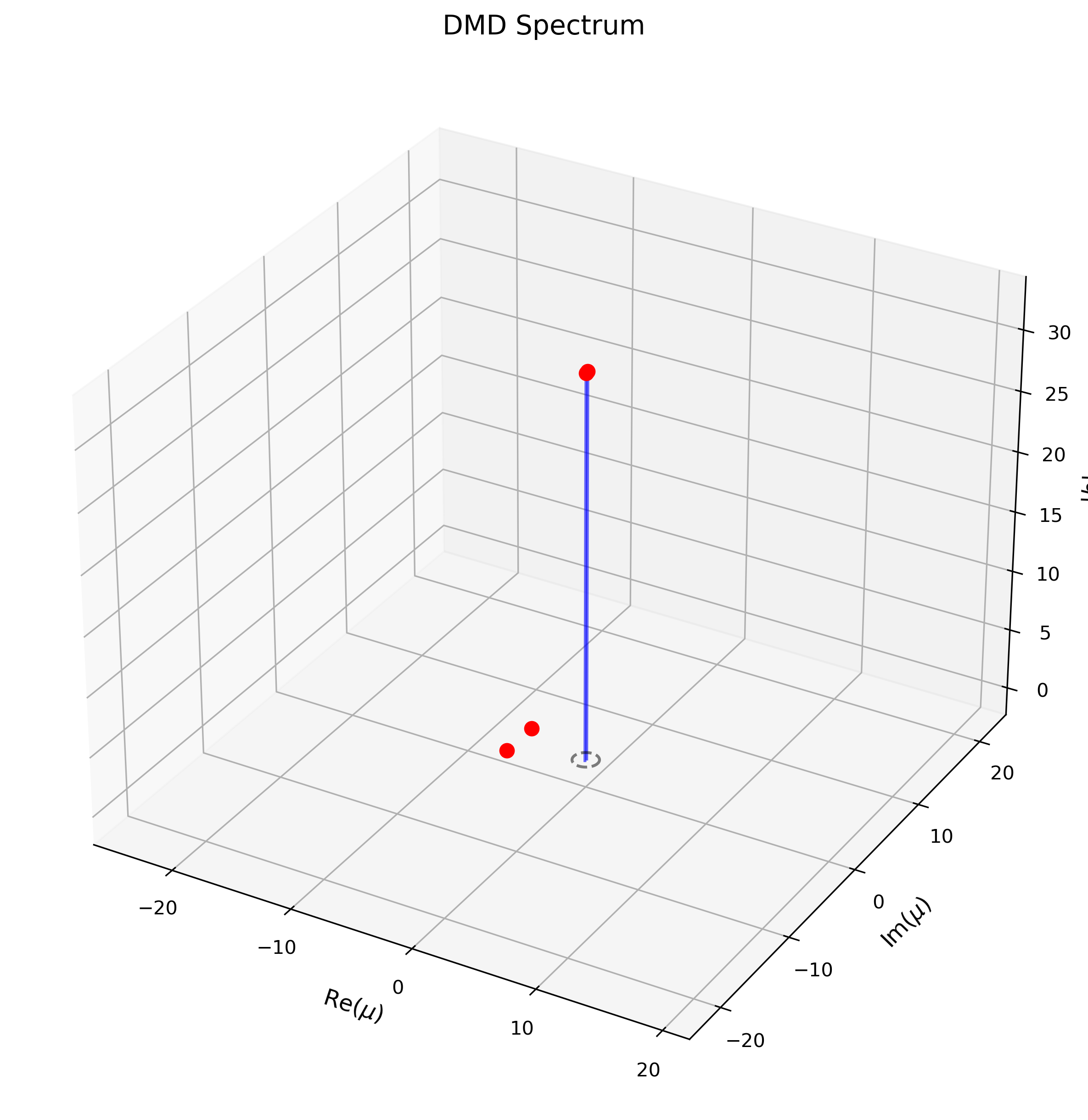
例如,对于我们之前使用的虚假流场, 有两个模态是衰减的,对应的增益为22左右, 有两个模态是发散的,对应的增益为$10^{-3}$量级。
总之,对于DMD的阶次选择,还需要根据具体的时间模态和增益来确定。