Dynamic Mode Decomposition #

基本概念 #

DMD（Dynamic Mode Decomposition）是一种数据矩阵分解方法，这个方法把数据矩阵当作是一个线性动力学系统的输出来看待。对于每个快照，假设有如下的线性动力学系统：

这里的$\mathbf{x}_i$和$\mathbf{x}_{i+1}$是数据矩阵中的两个相邻的快照。矩阵$A$是线性动力学系统的线性演化矩阵。 对于一般的数据矩阵，通常并不能拟合一个线性动力学系统。

接下来，我们把数据矩阵$D$分解为两个部分，前$n_t-1$个快照为初始状态，后$n_t-1$个快照为演化后的状态。

有

DMD分解的推导 #

如果我们对$\mathbf{X}_1$进行SVD分解，可以得到：

其中，$\widetilde{\mathbf{X}}_{1, \tau}$是$\mathbf{X}_1$的低秩（rank-$\tau$）近似。

完全求解$A$的问题可以弱化为求解矩阵$S$的问题。

我们对原始的$\mathbf{X}_2$进行变换，步骤如下：

带入SVD分解的结果

两边左乘$U^T$，得到：

两边右乘$V$，得到：

两边右乘$\Sigma^{-1}$，得到：

如此，我们即得到了$S$。

这里正定归一矩阵$U$，$U^T = U^{-1}$，就是前面的$Q$。 值得注意的是，这里的$U$并不一定是方阵， 相应的，$S$则为$\tau \times \tau$的矩阵。

对$S$进行特征值分解，可以得到：

其中，$\Phi$是$S$的特征向量矩阵，$M$是$S$的特征值矩阵。 一般而言，$M$和$\Phi$是复数矩阵。 因为$S$的大小为$\tau \times \tau$，所以只能近似拟合$A$的前$\tau$个特征值。

将对角矩阵$M$的对角元素记为$\mathbf{\mu}$，则有：

此处的$\omega_i$为相应脉动的复数频率，同样把这个向量记为$\mathbf{\omega}$。 有

下面，我们得到DMD的空间模态为：

这个式子的物理含义可以理解为，将特征向量矩阵$\Phi$变换到$U$的列（正交）基上。

DMD的增益矩阵为：

这里的$\mathbf{x}_1$是$\mathbf{X}_1$的第一个列向量，也就是初始状态。

我们把DMD的时间模态表达为矩阵$\mathbf{T}_{\text{modes}}$， 则有该矩阵的尺寸为$\tau \times n_t$，该矩阵的第$i$列即为DMD的第$i$个时间模态，通过如下公式计算：

此处，$k = \frac{t_i}{\Delta t}$，$\Delta t$为时间步长。因此，DMD要求时间步长$\Delta t$为常数。

值得注意的是，$\mathbf{T}_{\text{modes}}$的第$j$行对应一个频率（$\omega_j$）和一个增益（$b_j$）。

到这里就可以写出DMD的表达式：

这里，增益矩阵和时间模态写在同一个矩阵中。

算法实现 #

采用Eigen3库实现，计算的步骤和设计的主要矩阵大小如下：

1. 数据分组：$\mathbf{X}_1,\mathbf{X}_2, n_p \times n_t-1$
2. SVD分解：$\mathbf{X}_1 = U \Sigma V^T, \tau$
3. 相似矩阵：$S=U^T \mathbf{X}_2 V \Sigma^{-1}, \tau\times\tau$
4. 特征分解：$S = \Phi M \Phi^{-1}, \tau\times\tau$
5. 空间模态：$ \phi = U \Phi, n_p \times \tau$
6. 增益矩阵：$ \mathbf{b} = (\phi^T \phi)^{-1} \phi^T \mathbf{x}_1, \tau \times 1$
7. 频率向量：$\mathbb{\omega} = \ln \mathbf{\mu}, \tau \times 1$
8. 时间模态：$\mathbf{t}_i = \mathbf{b} e^{\omega k} = \mathbf{b} e ^{\omega t_i/ \Delta t}, i=1\ldots n_t$

实现 #

整个算法的最终接口与POD类似，输入数据，得到一个空间模态矩阵，一个时间系数（作为增益和时间模态的乘积），最终重建的近似数据为空间模态矩阵和时间系数的乘积。

#pragma once
#include <Eigen/Dense>
#include <complex>
#include <vector>

class DMD {
public:
    DMD() = default;

    // Compute DMD modes from snapshot matrices X1 (x[0:n-1]) and X2 (x[1:n])
    // r is the desired rank of the approximation
    void compute(const Eigen::MatrixXd& X1, const Eigen::MatrixXd& X2, int r);

    // Compute DMD modes from a single snapshot matrix X
    // This will automatically create X1 and X2 by splitting X
    void compute(const Eigen::MatrixXd& X, int r);

    // Predict future state at time t
    Eigen::VectorXcd predict(double t) const;

    // Reconstruct the data at specified timesteps
    Eigen::MatrixXcd reconstruct(const Eigen::VectorXd& timesteps) const;

    // Getters for DMD components
    const Eigen::MatrixXcd& modes() const { return modes_; }
    const Eigen::VectorXcd& eigenvalues() const { return eigenvalues_; }
    const Eigen::VectorXcd& amplitudes() const { return amplitudes_; }
    double dt() const { return dt_; }

private:
    Eigen::MatrixXcd modes_;        // DMD modes (Phi)
    Eigen::VectorXcd eigenvalues_;  // DMD eigenvalues (Lambda)
    Eigen::VectorXcd amplitudes_;   // Mode amplitudes (b)
    double dt_;                     // Time step between snapshots
    int rank_;                      // Rank of approximation
}; 

classDiagram
    class DMD {
        -Eigen::VectorXcd eigenvalues_
        -Eigen::MatrixXcd modes_
        -Eigen::VectorXcd amplitudes_
        -double dt_
        +void compute(const Eigen::MatrixXd &X1, const Eigen::MatrixXd &X2, int r)
        +void compute(const Eigen::MatrixXd &X, int r)
        +Eigen::VectorXcd predict(double t) const
        +Eigen::MatrixXcd reconstruct(const Eigen::VectorXd &timesteps) const
    }

结果展示 #

同样，DMD的计算结果可以可视化如下：

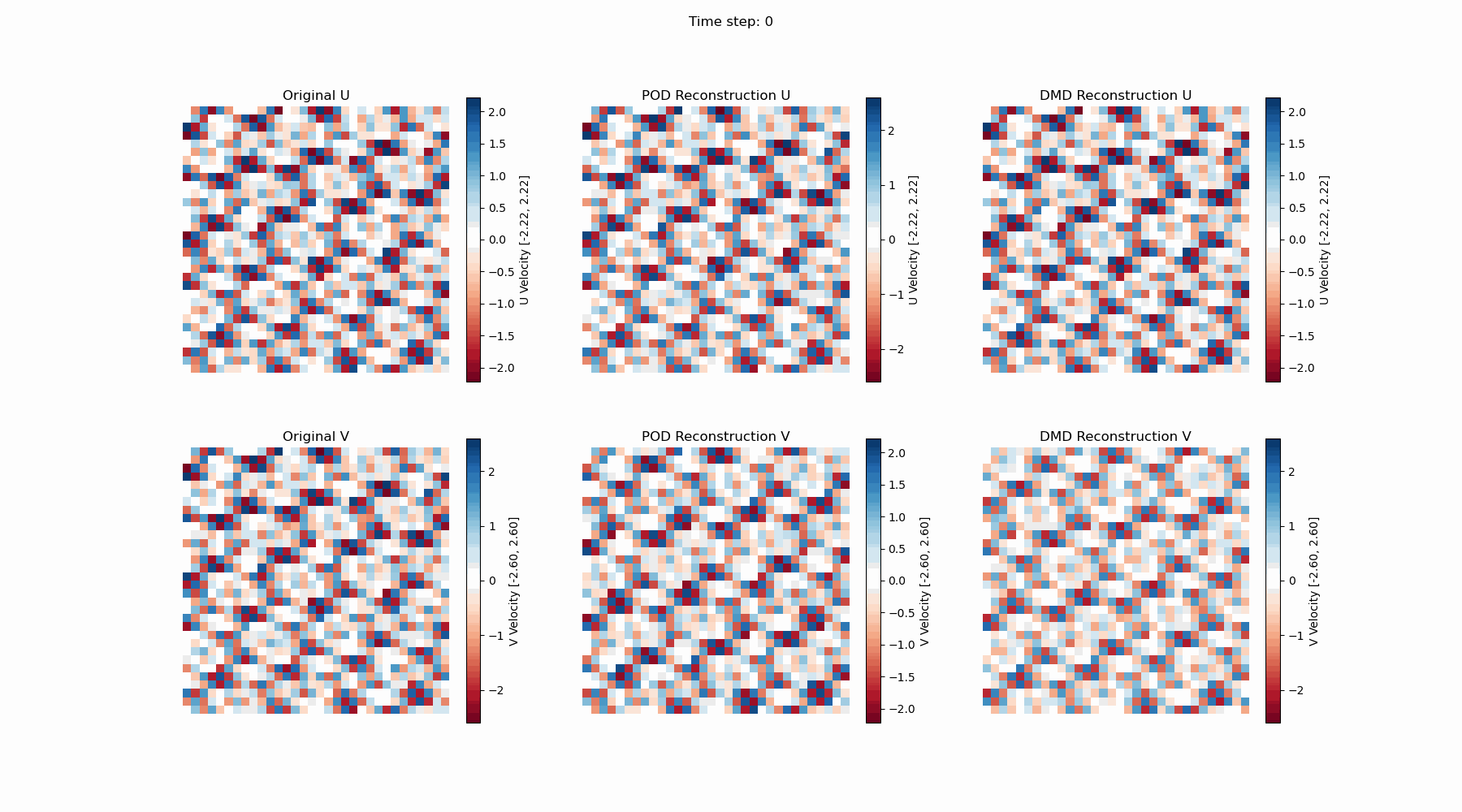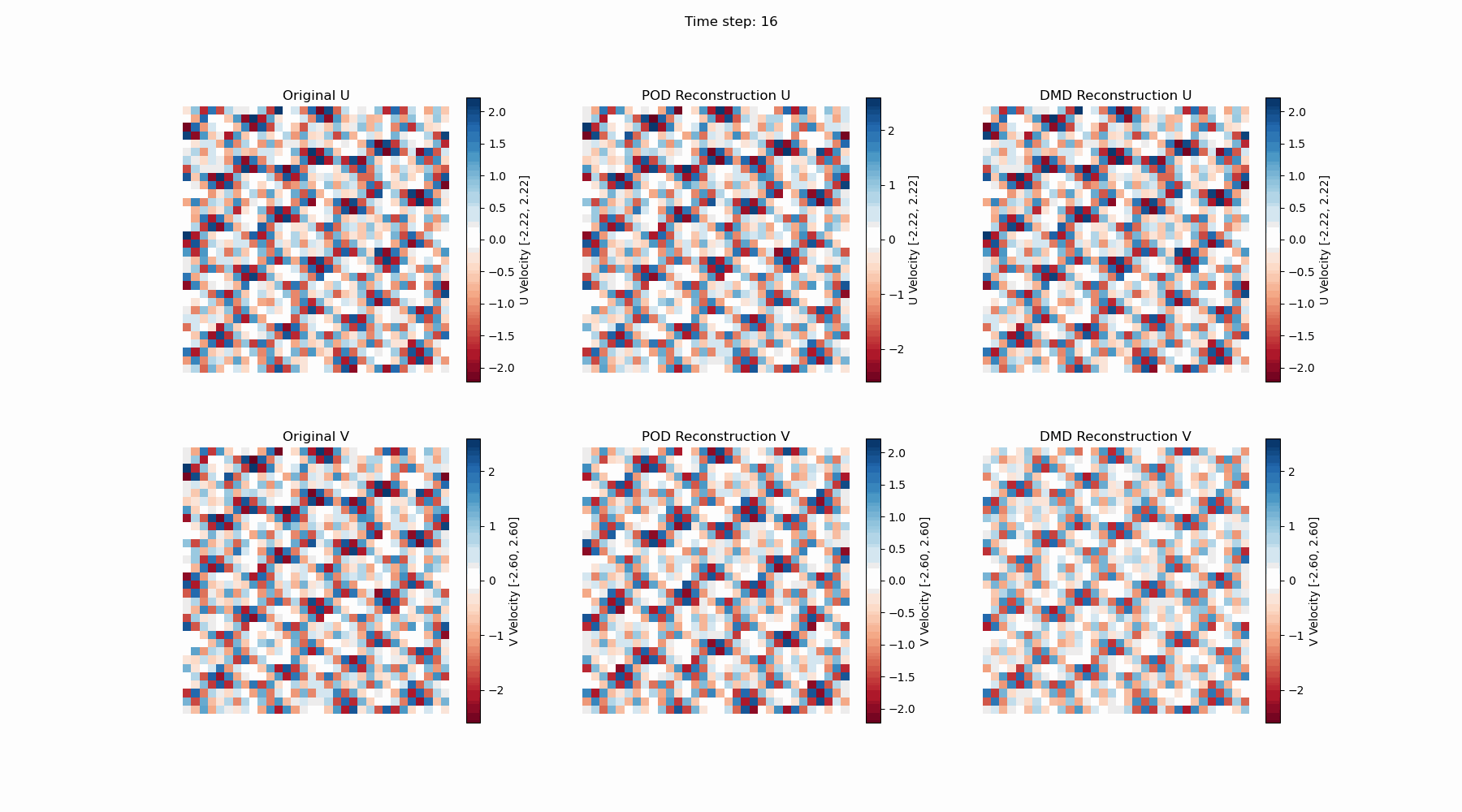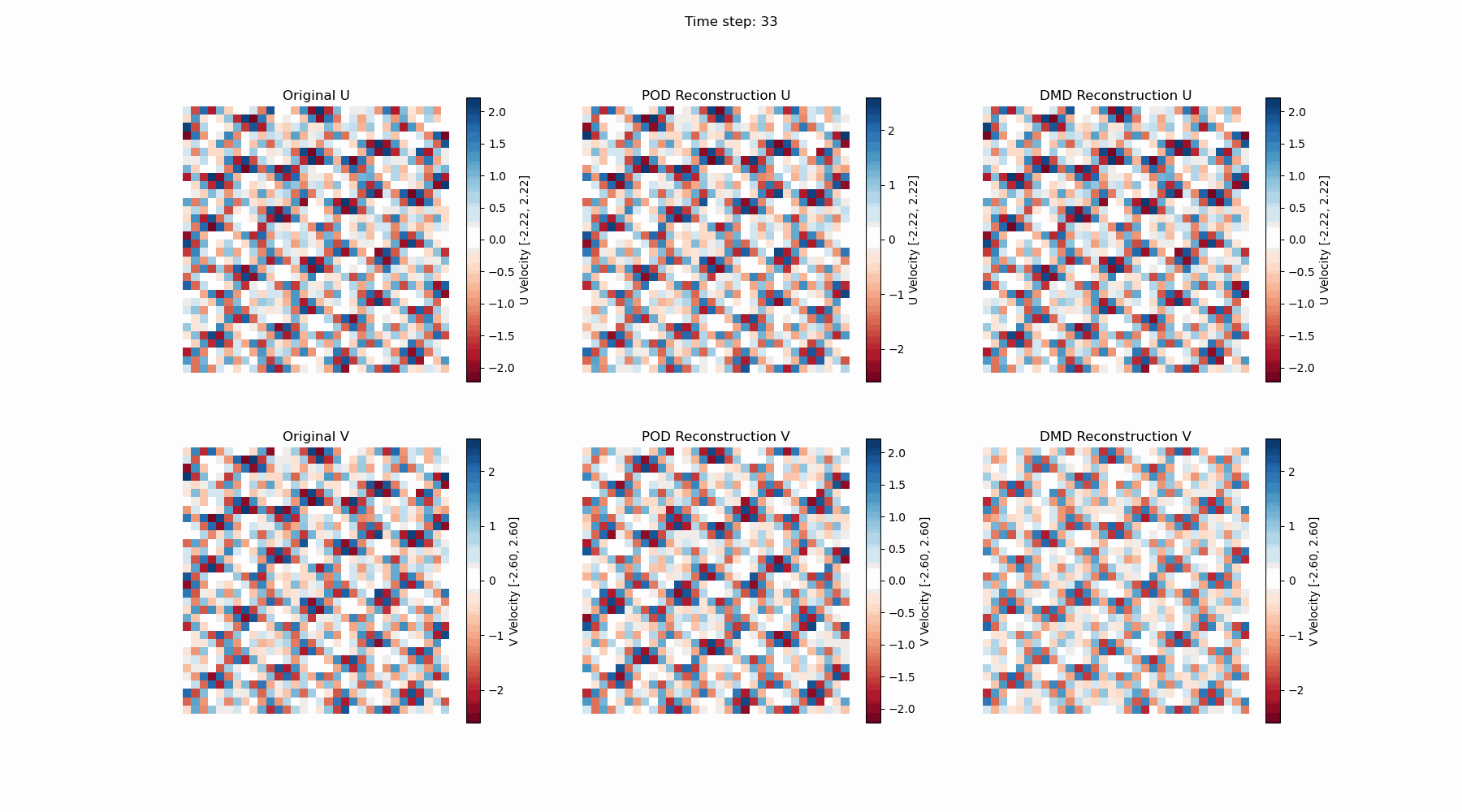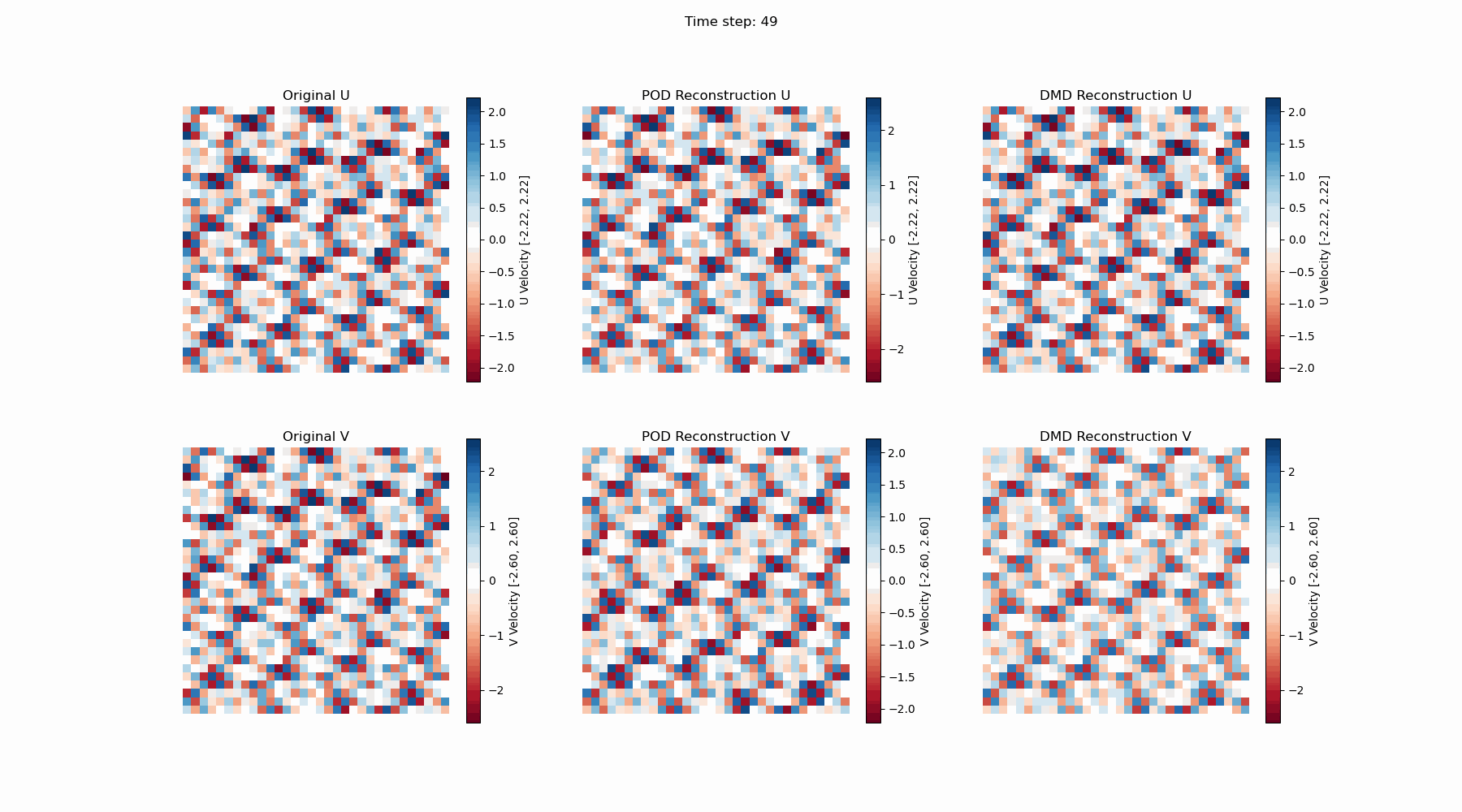
因为DMD的中间计算结果是复数矩阵，最终重建的结果中有一个而很小的虚部，对上面的算例，虚部的小于$1e-15$，可以忽略不计。

代码和运行 #

所有的代码，都可以在Github Repository中找到。

运行命令：

git clone https://github.com/qchen-fdii-cardc/fluiddecomposition.git
cd fluiddecomposition
cmake -B build .
cmake --build build
./build/debug/pod_demo
./build/debug/dmd_demo
python ./scripts/visualize_flow.py